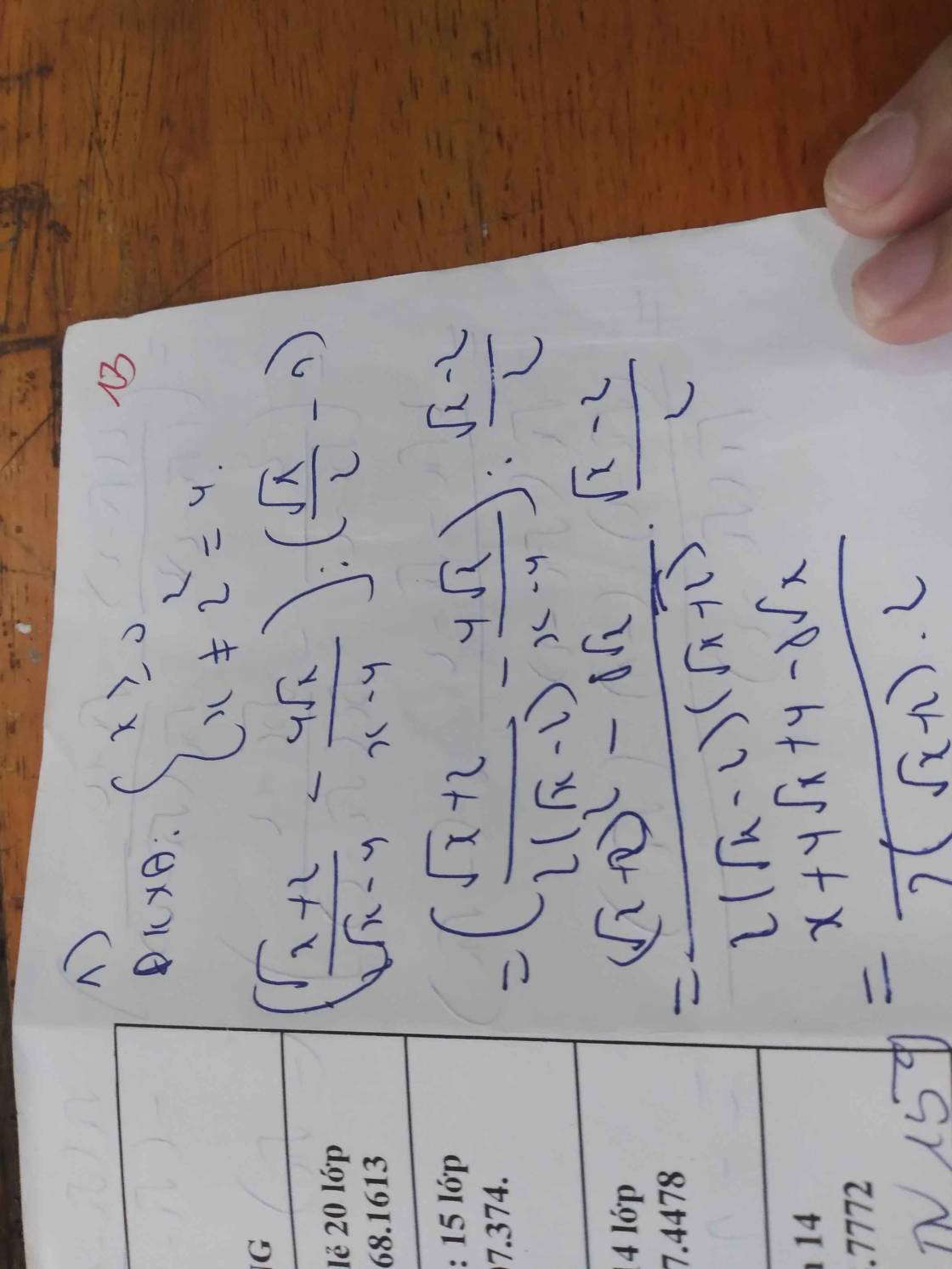
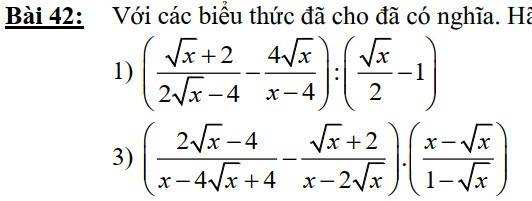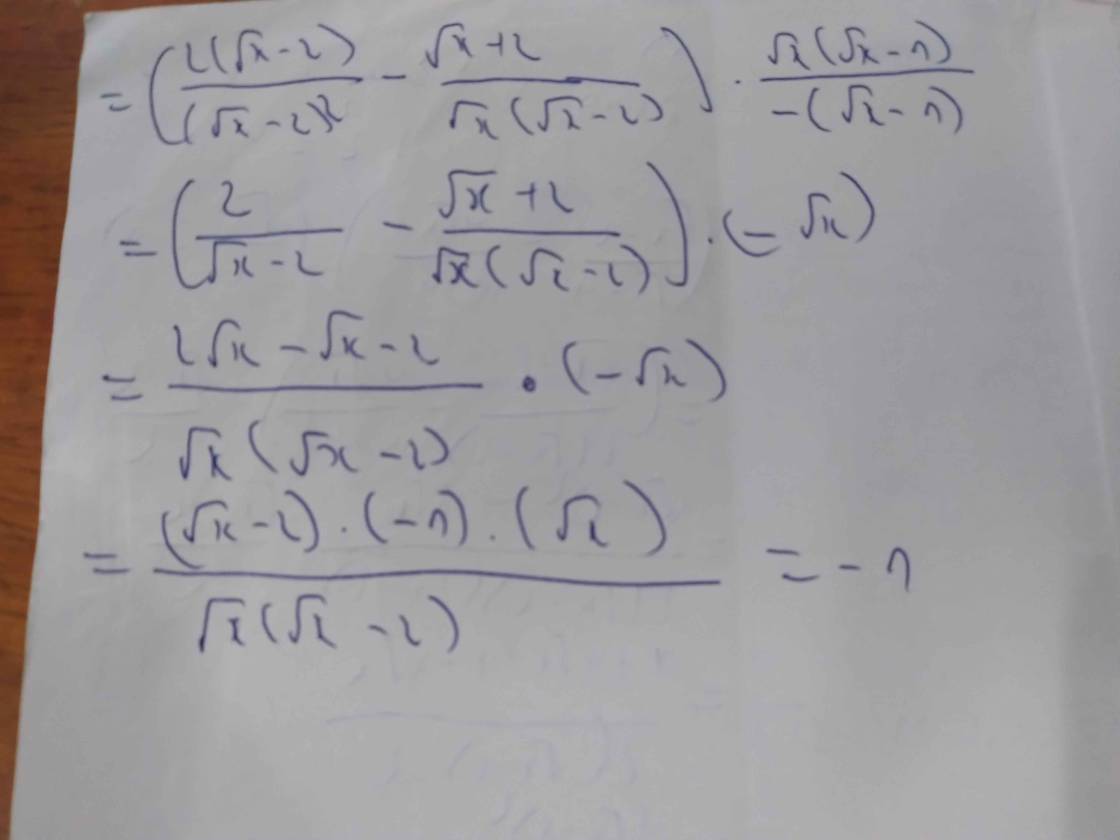1) \(\left(\dfrac{\sqrt{x}+2}{2\sqrt{x}-4}-\dfrac{4\sqrt{x}}{x-4}\right):\left(\dfrac{\sqrt{x}}{2}-1\right)\) (ĐK: \(x>0;x\ne4\))
\(=\left[\dfrac{\sqrt{x}+2}{2\left(\sqrt{x}-2\right)}-\dfrac{4\sqrt{x}}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\right]:\left(\dfrac{\sqrt{x}}{2}-\dfrac{2}{2}\right)\)
\(=\left[\dfrac{\left(\sqrt{x}+2\right)^2}{2\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}-\dfrac{4\sqrt{x}\cdot2}{2\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\right]:\dfrac{\sqrt{x}-2}{2}\)
\(=\dfrac{x+4\sqrt{x}+4-8\sqrt{x}}{2\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\cdot\dfrac{2}{\sqrt{x}-2}\)
\(=\dfrac{\left(\sqrt{x}-2\right)^2}{2\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\cdot\dfrac{2}{\sqrt{x}-2}\)
\(=\dfrac{1}{\sqrt{x}+2}\)
3) \(\left(\dfrac{2\sqrt{x}-4}{x-4\sqrt{x}+4}-\dfrac{\sqrt{x}+2}{x-2\sqrt{x}}\right)\cdot\left(\dfrac{x-\sqrt{x}}{1-\sqrt{x}}\right)\) (ĐK: \(x\ne4;x>0;x\ne1\))
\(=\left[\dfrac{2\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)^2}-\dfrac{\sqrt{x}+2}{\sqrt{x}\left(\sqrt{x}-2\right)}\right]\cdot\left(-\dfrac{\sqrt{x}-x}{1-\sqrt{x}}\right)\)
\(=\left[\dfrac{2}{\sqrt{x}-2}-\dfrac{\sqrt{x}+2}{\sqrt{x}\left(\sqrt{x}-2\right)}\right]\cdot\left[-\dfrac{\sqrt{x}\left(1-\sqrt{x}\right)}{1-\sqrt{x}}\right]\)
\(=\dfrac{2\sqrt{x}-\sqrt{x}-2}{\sqrt{x}\left(\sqrt{x}-2\right)}\cdot-\sqrt{x}\)
\(=\dfrac{\sqrt{x}-2}{\sqrt{x}\left(\sqrt{x}-2\right)}\cdot-\sqrt{x}\)
\(=-\dfrac{\sqrt{x}}{\sqrt{x}}\)
\(=-1\)