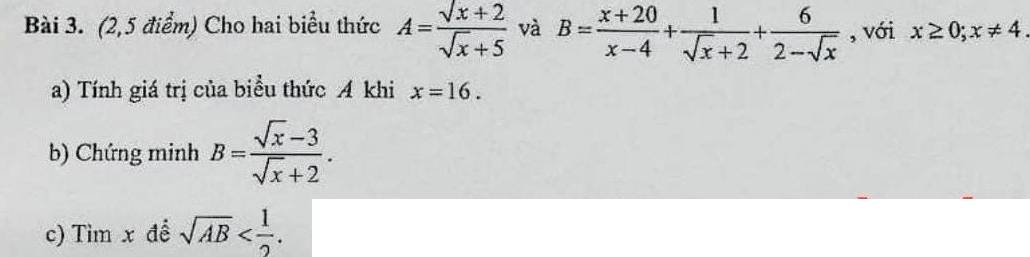`a)x=16` t/m đk, thay vào `A` có: `A=[\sqrt{16}+2]/[\sqrt{16}+5]=2/3`
`b)` Với `x >= 0,x ne 4` có:
`B=[x+20]/[(\sqrt{x}-2)(\sqrt{x}+2)]+[\sqrt{x}-2-6(\sqrt{x}+2)]/[(\sqrt{x}-2)(\sqrt{x}+2)]`
`B=[x+20+\sqrt{x}-2-6\sqrt{x}-12]/[(\sqrt{x}-2)(\sqrt{x}+2)]`
`B=[x-5\sqrt{x}+6]/[(\sqrt{x}-2)(\sqrt{x}+2)]`
`B=[(\sqrt{x}-2)(\sqrt{x}-3)]/[(\sqrt{x}-2)(\sqrt{x}+2)]`
`B=[\sqrt{x}-3]/[\sqrt{x}+2]` (đpcm)
`c)` Với `x >= 0,x ne 4` có:
`\sqrt{AB} < 1/2`
`<=>\sqrt{[(\sqrt{x}+2)(\sqrt{x}-3)]/[(\sqrt{x}+5)(\sqrt{x}+2)]} < 1/2`
`<=>\sqrt{[\sqrt{x}-3]/[\sqrt{x}+5]} < 1/2`
`<=>[\sqrt{x}-3]/[\sqrt{x}+5] < 1/4`
`<=>[4\sqrt{x}-12-\sqrt{x}-5]/[4(\sqrt{x}+5)] < 0`
`<=>[3\sqrt{x}-17]/[\sqrt{x}+5] < 0`
Với `x >= 0,x ne 4=>\sqrt{x}+5 > 0`
`=>3\sqrt{x}-17 < 0`
`<=>\sqrt{x} < 17/3`
`<=>x < 289/9`
Mà `x >= 0,x ne 4`
`=>0 <= x < 289/9,x ne 4`.
a) x=16
=> \(A=\dfrac{\sqrt{16}+2}{\sqrt{16}+5}=\dfrac{6}{9}=\dfrac{2}{3}\)
b) \(B=\dfrac{x+20+\sqrt{x}-2-6\left(\sqrt{x}+2\right)}{x-4}\)
\(=\dfrac{x-5\sqrt{x}+6}{x-4}=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}-3}{\sqrt{x+2}}\)
c) \(\sqrt{AB}=\sqrt{\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-3\right)}{\left(\sqrt{x+5}\right)\left(\sqrt{x}+2\right)}}=\sqrt{\dfrac{\sqrt{x}-3}{\sqrt{x}+5}}\left(đk:x\ge9\right)\)
\(\sqrt{AB}< \dfrac{1}{2}\Rightarrow\sqrt{\dfrac{\sqrt{x}-3}{\sqrt{x}+5}}< \dfrac{1}{2}\)
\(\Leftrightarrow\sqrt{x}+5>4\left(\sqrt{x}-3\right)\)
\(\Leftrightarrow3\sqrt{x}< 17\)
\(\Leftrightarrow\sqrt{x}< \dfrac{17}{3}\) \(\Rightarrow0\le x< \dfrac{289}{3}\)