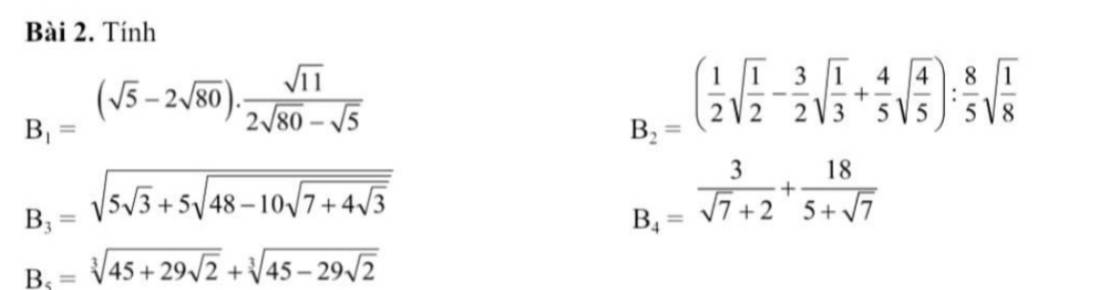
\(B1=\left(\sqrt{5}-8\sqrt{5}\right)\cdot\dfrac{\sqrt{11}}{8\sqrt{5}-\sqrt{5}}\)
\(=\dfrac{-7\sqrt{5}}{7\sqrt{5}}\cdot\sqrt{11}=-\sqrt{11}\)
\(B2=\left(\dfrac{1}{2\sqrt{2}}-\dfrac{\sqrt{3}}{2}+\dfrac{4}{5}\cdot\dfrac{2}{\sqrt{5}}\right):\dfrac{8}{5\cdot2\sqrt{2}}\)
\(=\left(\dfrac{\sqrt{2}}{4}-\dfrac{2\sqrt{3}}{4}+\dfrac{8\sqrt{5}}{25}\right)\cdot\dfrac{10\sqrt{2}}{8}\)
\(=\dfrac{25\left(\sqrt{2}-2\sqrt{3}\right)+32\sqrt{5}}{100}\cdot\dfrac{10\sqrt{2}}{8}\)
\(=\dfrac{\sqrt{2}\left(25\sqrt{2}-50\sqrt{3}+32\sqrt{5}\right)}{80}\)
\(B3=\sqrt{5\sqrt{3}+5\sqrt{48-10\left(2+\sqrt{3}\right)}}\)
\(B3=\sqrt{5\sqrt{3}+5\sqrt{28-10\sqrt{3}}}\)
\(B3=\sqrt{5\sqrt{3}+5\left(5-\sqrt{3}\right)}=\sqrt{25}=5\)
\(B_4=\dfrac{3\left(\sqrt{7}-2\right)}{7-4}+\dfrac{18\left(5-\sqrt{7}\right)}{18}\)
\(=\sqrt{7}-2+5-\sqrt{7}=3\)