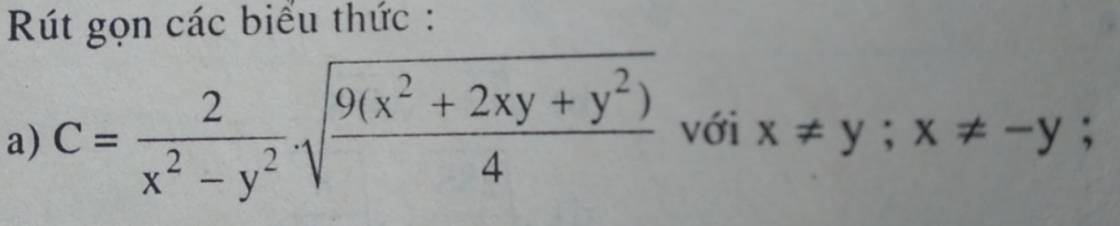\(C=\dfrac{2}{x^2-y^2}\cdot\sqrt{\dfrac{9\left(x^2+2xy+y^2\right)}{4}}\)
\(C=\dfrac{2}{\left(x+y\right)\left(x-y\right)}\cdot\sqrt{\dfrac{3^2\cdot\left(x+y\right)^2}{2^2}}\)
\(C=\dfrac{2}{\left(x+y\right)\left(x-y\right)}\cdot\sqrt{\left[\dfrac{3\left(x+y\right)}{2}\right]^2}\)
\(C=\dfrac{2}{\left(x+y\right)\left(x-y\right)}\cdot\left|\dfrac{3\left(x+y\right)}{2}\right|\)
TH1: \(x>-y\)
\(C=\dfrac{2}{\left(x+y\right)\left(x-y\right)}\cdot\dfrac{3\left(x+y\right)}{2}\)
\(C=\dfrac{3\cdot2\cdot\left(x+y\right)}{2\cdot\left(x+y\right)\cdot\left(x-y\right)}\)
\(C=\dfrac{3}{x-y}\)
TH2: \(x< -y\)
\(C=\dfrac{2}{\left(x+y\right)\left(x-y\right)}\cdot\dfrac{-3\left(x+y\right)}{2}\)
\(C=\dfrac{-3\left(x+y\right)}{\left(x+y\right)\left(x-y\right)}\)
\(C=\dfrac{-3}{x-y}\)
\(C=\dfrac{3}{y-x}\)
\(C=\dfrac{2}{x^2-y^2}\sqrt[]{\dfrac{9\left(x^2+2xy+y^2\right)}{4}}\left(x\ne\pm y\right)\)
\(\Leftrightarrow C=\dfrac{2}{\left(x+y\right)\left(x-y\right)}\sqrt[]{\dfrac{9\left(x+y\right)^2}{4}}\)
\(\Leftrightarrow C=\dfrac{2}{\left(x+y\right)\left(x-y\right)}.\dfrac{3\left|x+y\right|}{2}\)
\(\Leftrightarrow C=\dfrac{3\left|x+y\right|}{\left(x+y\right)\left(x-y\right)}\)
\(\Leftrightarrow C=\left[{}\begin{matrix}\dfrac{3\left(x+y\right)}{\left(x+y\right)\left(x-y\right)}=\dfrac{3}{x-y}\left(x>-y\right)\\\dfrac{-3\left(x+y\right)}{\left(x+y\right)\left(x-y\right)}=\dfrac{-3}{x-y}\left(x< -y\right)\end{matrix}\right.\)