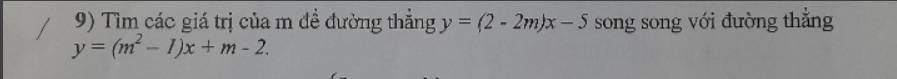Hai đường thẳng này song song, khi và chỉ khi:
2-2m= m2 - 1
<=> m2+2m - 3= 0
<=>m2 - m +3m - 3=0
<=> m(m-1)+3(m-1)=0
<=>(m+3)(m-1)=0
<=> m+3=0 hoặc m-1=0
<=> m=-3 hoặc m=1
Vậy: m=-3 hoặc m=1
\(\left\{{}\begin{matrix}\left(d_1\right):y=\left(2-2m\right)x-5\\\left(d_2\right):y=\left(m^2-1\right)x+m-2\end{matrix}\right.\)
Để \(\left(d_1\right)//\left(d_2\right)\) \(\Leftrightarrow\left\{{}\begin{matrix}2-2m=m^2-1\\m-2\ne-5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2+2m-3=0\\m\ne-3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m=1\\m=-3\left(loại\right)\end{matrix}\right.\\m\ne-3\end{matrix}\right.\)
\(\Leftrightarrow m=1\)
Vậy \(m=1\) thỏa mãn đề bài