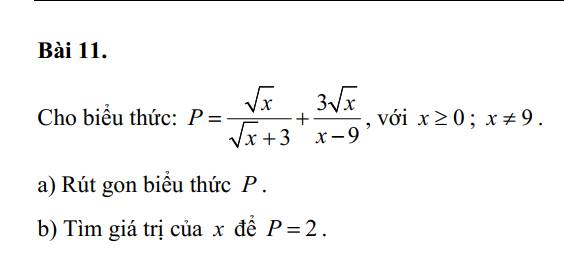Question

Answer 1

a)

\(P=\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{x-9}+\dfrac{3\sqrt{x}}{x-9}\\=\dfrac{x-3\sqrt{x}}{x-9}+\dfrac{3\sqrt{x}}{x-9}\\ =\dfrac{x-3\sqrt{x}+3\sqrt{x}}{x-9}\\ =\dfrac{x}{x-9}\)

b)

Để `P=2` thì:

\(\dfrac{x}{x-9}=2\\ \Leftrightarrow2x-18-x=0\\ \Leftrightarrow x-18=0\\ \Leftrightarrow x=18\)

 

Answer 2

a: \(P=\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)+3\sqrt{x}}{x-9}=\dfrac{x-3\sqrt{x}+3\sqrt{x}}{x-9}=\dfrac{x}{x-9}\)

b: P=2

=>2x-18=x

=>x=18(nhận)