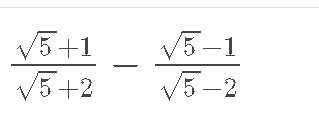Question

Answer 1

\(\dfrac{\sqrt{5}+1}{\sqrt{5}+2}-\dfrac{\sqrt{5}-1}{\sqrt{5}-2}\)

\(=\dfrac{\left(\sqrt{5}+1\right)\left(\sqrt{5}-2\right)}{\left(\sqrt{5}+2\right)\left(\sqrt{5}-2\right)}-\dfrac{\left(\sqrt{5}-1\right)\left(\sqrt{5}+2\right)}{\left(\sqrt{5}-2\right)\left(\sqrt{5}+2\right)}\)

\(=\dfrac{\left(\sqrt{5}+1\right)\left(\sqrt{5}-2\right)-\left(\sqrt{5}-1\right)\left(\sqrt{5}+2\right)}{\left(\sqrt{5}+2\right)\left(\sqrt{5}-2\right)}\)

\(=\dfrac{\left(5-2\sqrt{5}+\sqrt{5}-2\right)-\left(5+2\sqrt{5}-\sqrt{5}-2\right)}{\left(\sqrt{5}\right)^2-2^2}\)

\(=\dfrac{5-\sqrt{5}-2-5-\sqrt{5}+2}{1}\)

\(=-2\sqrt{5}\)

Answer 2

\(=\dfrac{\left(\sqrt{5}+1\right)\left(\sqrt{5}-2\right)-\left(\sqrt{5}-1\right)\left(\sqrt{5}+2\right)}{5-4}\)

\(=\dfrac{5-2\sqrt{5}+\sqrt{5}-2-5-2\sqrt{5}+\sqrt{5}+2}{1}\)

\(=-2\sqrt{5}\)