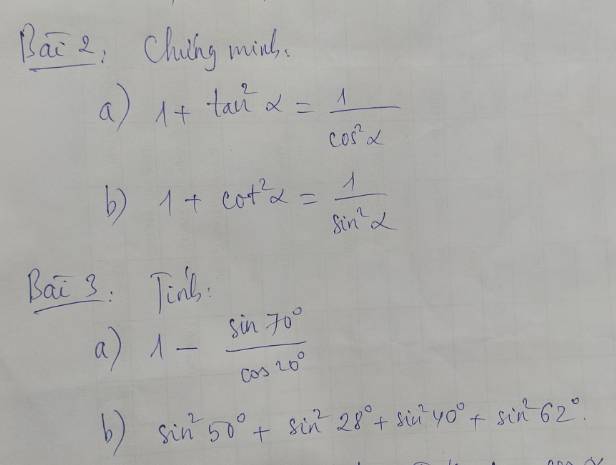3:
a: \(1-\dfrac{sin70}{cos20}=1-\dfrac{sin70}{sin70}\)
=1-1=0
b; \(=sin^250^0+sin^240^0+sin^228^0+sin^262^0\)
\(=sin^250^0+cos^250^0+sin^228^0+cos^228^0\)
=1+1
=2
Bài 2.
(a) Nhân cả vế trái và vế phải cho \(cos^2\alpha\), ta được:
\(cos^2\alpha\left(1+\dfrac{sin^2\alpha}{cos^2\alpha}\right)=1\Leftrightarrow sin^2\alpha+cos^2\alpha=1\) (luôn đúng).
Vậy: Ta có điều phải chứng minh.
(b) Nhân cả vế trái và vế phải cho \(sin^2\alpha\), ta được:
\(sin^2\alpha\left(1+\dfrac{cos^2\alpha}{sin^2\alpha}\right)=1\Leftrightarrow sin^2\alpha+cos^2\alpha=1\) (luôn đúng).
Vậy: Ta có điều phải chứng minh.
Bài 3.
(a) \(1-\dfrac{sin70^o}{cos20^o}=1-\dfrac{sin70^o}{sin\left(90^o-20^o\right)}=1-1=0\)
(b) \(sin^250^o+sin^228^o+sin^240^o+sin^262^o\)
\(=cos^2\left(90^o-50^o\right)+cos^2\left(90^o-28^o\right)+sin^240^o+sin^262^o\)
\(=cos^240^o+cos^262^o+sin^240^o+sin^262^o\)
\(=\left(sin^240^o+cos^240^o\right)+\left(sin^262^o+cos^262^o\right)\)
\(=1+1=2\)