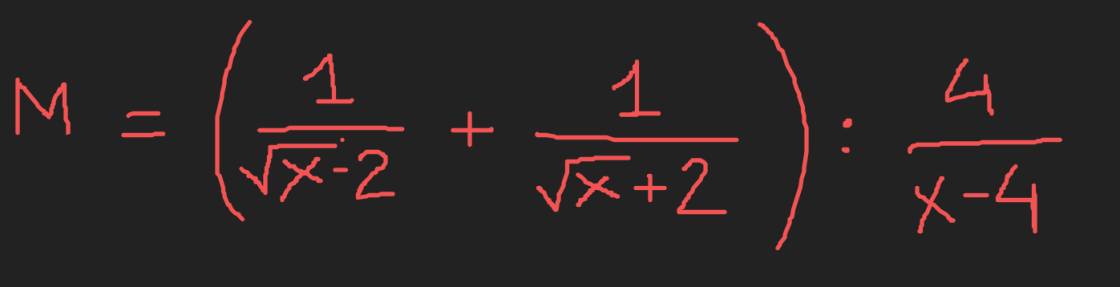\(M=\left(\dfrac{1}{\sqrt{x}-2}+\dfrac{1}{\sqrt{x}+2}\right):\dfrac{4}{x-4}\left(dk:x\ge0,x\ne4\right)\)
\(=\dfrac{\sqrt{x}+2+\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}.\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}{4}\)
\(=\dfrac{2\sqrt{x}}{4}\)
\(=\dfrac{\sqrt{x}}{2}\)
Vậy \(M=\dfrac{\sqrt{x}}{2}\) với \(x\ge0,x\ne4\)
ĐK: \(x\ge0;x\ne4\)
Khi đó:
\(M=\left(\dfrac{\sqrt{x}+2}{x-4}+\dfrac{\sqrt{x}-2}{x-4}\right).\dfrac{x-4}{4}\\ =\left(\dfrac{\sqrt{x}+2+\sqrt{x}-2}{x-4}\right).\dfrac{x-4}{4}\\ =\dfrac{2\sqrt{x}\left(x-4\right)}{\left(x-4\right).2.2}\\ =\dfrac{\sqrt{x}}{2}\)
\(ĐK:x\ne4\\ M=\left(\dfrac{1}{\sqrt{x}-2}+\dfrac{1}{\sqrt{x}+2}\right):\dfrac{4}{x-4}\\ =\dfrac{\left(\sqrt{x}+2\right)+\left(\sqrt{x}-2\right)}{x-4}.\dfrac{\left(x-4\right)}{4}\\ =\dfrac{2\sqrt{x}\left(x-4\right)}{4\left(x-4\right)}=\dfrac{\sqrt{x}\left(x-4\right)}{2\left(x-2\right)}\)