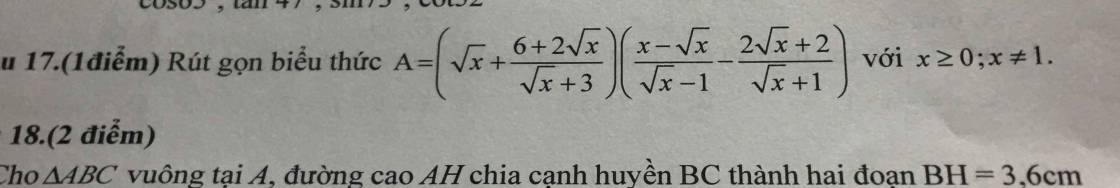\(=\left(\dfrac{\sqrt{x}\left(\sqrt{x}+3\right)+6+2\sqrt{x}}{\sqrt{x}+3}\right)\left(\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\sqrt{x}-1}-\dfrac{2\left(\sqrt{x}+1\right)}{\sqrt{x}+1}\right)\\ =\dfrac{x+3\sqrt{x}+6+2\sqrt{x}}{\sqrt{x}+3}.\left(\sqrt{x}-2\right)\\ =\dfrac{\sqrt{x}\left(\sqrt{x}+3\right)+2\left(3+\sqrt{x}\right)}{\sqrt{x}+3}.\left(\sqrt{x}-2\right)\\ =\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}+3\right)}{\sqrt{x}+3}.\left(\sqrt{x}-2\right)\\ =\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)\\ =x-4\)
\(A=\left(\sqrt{x}+\dfrac{6+2\sqrt{x}}{\sqrt{x}+3}\right)\left(\dfrac{x-\sqrt{x}}{\sqrt{x}-1}-\dfrac{2\sqrt{x}+2}{\sqrt{x}+1}\right)\)
\(A=\left(\sqrt{x}+\dfrac{2\left(3+\sqrt{x}\right)}{\sqrt{x}+3}\right)\left(\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\sqrt{x}-1}-\dfrac{2\left(\sqrt{x}+1\right)}{\sqrt{x}+1}\right)\)
\(A=\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)\)
\(A=\left(\sqrt{x}\right)^2-2^2\)
\(A=x-4\)
Câu 17:
`(sqrt x + (6+2sqrtx)/(sqrtx+3))((x-sqrtx)/(sqrtx-1) - (2sqrtx+2)/(sqrtx+1))`
`= (sqrtx + (2(sqrtx+3))/(sqrtx+3))(sqrtx(sqrtx-1))/(sqrtx-1) - (2(sqrtx+1))/(sqrtx+1))`.
`= (sqrtx+2)(sqrtx-2)`
`= x-4`.
ĐKXĐ: x ≥ 0; x ≠ 1
\(A=\left(\sqrt{x}+\dfrac{6+2\sqrt{x}}{\sqrt{x}+3}\right)\left(\dfrac{x-\sqrt{x}}{\sqrt{x}-1}-\dfrac{2\sqrt{x}+2}{\sqrt{x}+1}\right)\\ =\left(\sqrt{x}+\dfrac{6+2\sqrt{x}}{\sqrt{x}+3}\right)\cdot\dfrac{x-3\sqrt{x}+2}{\sqrt{x}-1}\\ =\left(\sqrt{x}+\dfrac{6+2\sqrt{x}}{\sqrt{x}+3}\right)\cdot\left(\sqrt{x}-2\right)\\ =x+\dfrac{6\sqrt{x}+2x}{\sqrt{x}+3}-2\sqrt{x}-\dfrac{12+4\sqrt{x}}{\sqrt{x}+3}\\ =x+\dfrac{2x+2\sqrt{x}-12}{\sqrt{x}+3}-2\sqrt{x}\\ =x+2\sqrt{x}-4-2\sqrt{x}\\ =x-4\)