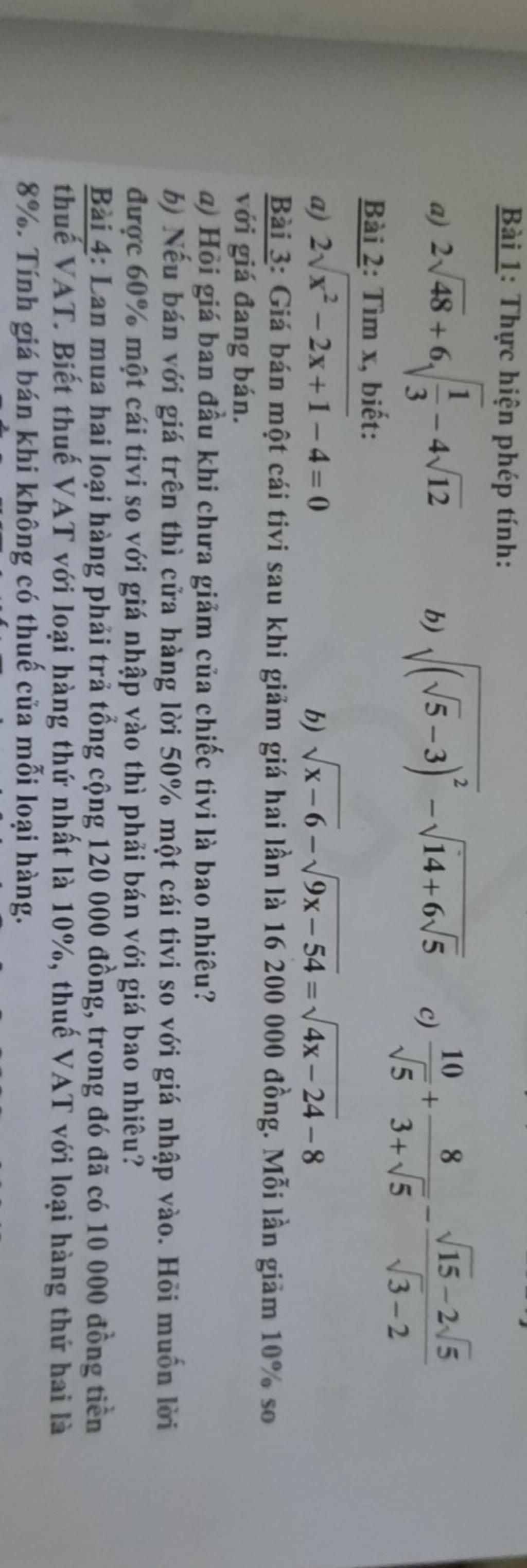Bài 2:
`a, 2 sqrt(x^2-2x+1) -4 = 0`.
`<=> 2 sqrt(x^2-2x+1) = 4`.
`<=> sqrt((x-1)^2) = 2.`
`<=> x - 1 = 2.`
`<=> x = 3`.
Vậy `x =3.`
`b, sqrt(x-6) - sqrt(9x-54) = sqrt(4x-24) -8`
Đk: `x >=6`.
`<=> sqrt(x-6) - 3 sqrt(x-6) = 2 sqrt(x-6) - 8`
`<=> 4 sqrt(x-6) = 8`.
`<=> sqrt(x-6) = 2`.
`<=> x - 6 = 4`.
`<=> x = 10`.
Vậy `x = 10.`
Bài 3:
a) Giá sau khi giảm lần đầu:
\(16200000:\left(100\%-10\%\right)=16200000:90\%=18000000\) (đồng)
Giá ban đầu của chiếc tivi:
\(18000000:\left(100\%-10\%\right)=18000000:90\%=20000000\) (đồng)
b) Giá nhập vào của tivi:
\(16200000:3.2=10800000\) (đồng)
Nếu muốn lãi 60% của giá nhập vào thì giá bán của tivi là:
\(10800000+10800000.60\%=17280000\) (đồng)
Bài 2:
`2 sqrt 48 + 6 sqrt(1/3) -4 sqrt 12`.
`= 2 sqrt(16.3) + 2.sqrt(1/3.3^2) - 4 .sqrt(4.3)`
`= 8sqrt 3 + 2 sqrt 3 - 4 sqrt 3`.
`= 6 sqrt 3.`
`b, sqrt((sqrt 5 -3)^2) - sqrt(14+6sqrt5)`.
`= 3 - sqrt 5 - sqrt(9+6sqrt 5 + 5).`
`= 3 - sqrt 5 - 3 - sqrt 5`.
`= - 2 sqrt 5`.
`c, 10/sqrt 5 + 8/(3 + sqrt 5) - (sqrt 15 - 2 sqrt 5)/(sqrt 3 -2)`.
`= sqrt100/sqrt 5 + (2.(3 + sqrt 5)(3-sqrt5))/(3+ sqrt 5) - (sqrt3.sqrt5 - 2 sqrt 5)/(sqrt3-2)`
`= sqrt 20 + 2.(3- sqrt5) - sqrt5.`
`= 2 sqrt 5 + 6 - 2 sqrt 5- sqrt 5`.
`= -sqrt 5 + 6`.
Bài 4:
Gọi giá gốc của mặt hàng thứ nhất là \(x\) (đồng) (\(0< x< 110000\) đồng)
\(\Rightarrow\) Giá gốc của mặt hàng thứ hai là: \(\text{110000 – x}\) (đồng)
Thuế VAT của mặt hàng thứ nhất bằng: \(\text{10%.x = 0,1x}\) (đồng).
Thuế VAT của mặt hàng thứ hai bằng: \(\text{8%.(110000 – x) = 0,08.(110000 – x)}\) (đồng).
Thuế VAT của cả hai mặt hàng bằng: \(\text{0,1x + 0,08(110000 – x)}\) (nghìn đồng).
Theo đề bài, tổng thuế VAT của cả hai mặt hàng là 10000 đồng nên ta có phương trình:
\(\text{0,1x + 0,08(110000 – x) = 10000}\)
⇔ \(\text{0,1x + 8800 – 0,08x = 10000}\)
⇔ \(\text{0,02x = 1200}\)
⇔ \(\text{x = 60000}\) (nhận).
Vậy không kể VAT thì giá của mặt hàng thứ nhất là 60000 đồng, giá của mặt hàng thứ hai là 110000 – 60000 = 50000 đồng.