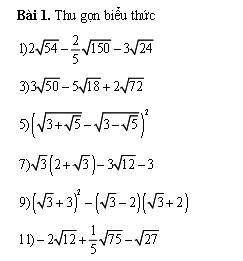\(1,\\ 2\sqrt{54}-\dfrac{2}{5}\sqrt{150}-3\sqrt{24}=2\sqrt{2.3.3^2}-\dfrac{2}{5}.\sqrt{2.3.5^2}-3.\sqrt{2^2.2.3}\\ =2.3.\sqrt{6}-\dfrac{2}{5}.5.\sqrt{6}-3.2.\sqrt{6}=6\sqrt{6}-2\sqrt{6}-6\sqrt{6}=-2\sqrt{6}\)
\(3,\\ 3\sqrt{50}-5\sqrt{18}+2\sqrt{72}=3\sqrt{5^2.2}-5\sqrt{3^2.2}+2\sqrt{6^2.2}\\ =3.5\sqrt{2}-5.3\sqrt{2}+2.6\sqrt{2}=15\sqrt{2}-15\sqrt{2}+12\sqrt{2}=12\sqrt{2}\)
5: \(=3+\sqrt{5}+3-\sqrt{5}-2\sqrt{\left(3+\sqrt{5}\right)\left(3-\sqrt{5}\right)}\)
=6-2*2=2
7: \(=2\sqrt{3}+3-6\sqrt{3}-3=-4\sqrt{3}\)
9: \(=12+6\sqrt{3}-3+4=13+6\sqrt{3}\)
11: \(=-4\sqrt{3}+\sqrt{3}-3\sqrt{3}=-6\sqrt{3}\)
\(7,\sqrt{3}\left(2+\sqrt{3}\right)-3\sqrt{12}-3\\ =\sqrt{3.2^2}+3-3\sqrt{12}-3=\sqrt{12}+\left(3-3\right)-3\sqrt{12}=-2\sqrt{12}\\ 11,-2\sqrt{12}+\dfrac{1}{5}\sqrt{75}-\sqrt{27}=-2\sqrt{2^2.3}+\dfrac{1}{5}\sqrt{3.5^2}-\sqrt{3^2.3}\\ =-2.2\sqrt{3}+\dfrac{1}{5}.5\sqrt{3}-3.\sqrt{3}=-4\sqrt{3}+\sqrt{3}-3\sqrt{3}=-6\sqrt{3}\)