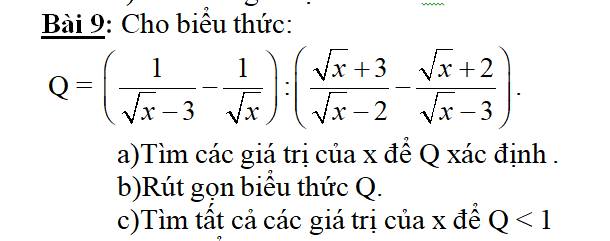\(a,Q\) xác định khi và chỉ khi \(\left\{{}\begin{matrix}\sqrt{x}\ne0\\\sqrt{x}-3\ne0\\\sqrt{x}-2\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x>0\\x\ne9\\x\ne4\end{matrix}\right.\)
\(b,Q=\left(\dfrac{1}{\sqrt{x}-3}-\dfrac{1}{\sqrt{x}}\right):\left(\dfrac{\sqrt{x}+3}{\sqrt{x}-2}-\dfrac{\sqrt{x}+2}{\sqrt{x}-3}\right)\)
\(=\dfrac{\sqrt{x}-\left(\sqrt{x}-3\right)}{\sqrt{x}\left(\sqrt{x}-3\right)}:\dfrac{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)-\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{3}{\sqrt{x}\left(\sqrt{x}-3\right)}.\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}{\left(x-9\right)-\left(x-4\right)}\)
\(=\dfrac{3}{\sqrt{x}}.\dfrac{\sqrt{x}-2}{x-9-x+4}\)
\(=\dfrac{3}{\sqrt{x}}.\dfrac{\sqrt{x}-2}{-5}\)
\(=\dfrac{3\left(\sqrt{x}-2\right)}{-5\sqrt{x}}\)
\(c,Q< 1\Leftrightarrow\dfrac{3\left(\sqrt{x}-2\right)}{-5\sqrt{x}}< 1\)
\(\Rightarrow\dfrac{-3\sqrt{x}+6-5\sqrt{x}}{5\sqrt{x}}< 0\)
\(\Rightarrow-8\sqrt{x}< -6\)
\(\Rightarrow\sqrt{x}>\dfrac{6}{8}\Rightarrow x>\dfrac{9}{16}\)