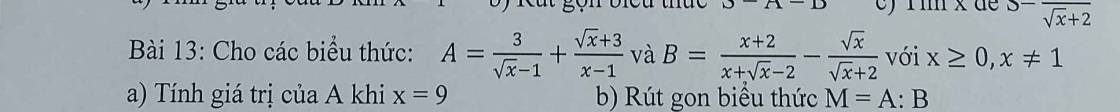Bài 13 :
\(a,x=9\Rightarrow A=\dfrac{3}{\sqrt{9}-1}+\dfrac{\sqrt{9}+3}{9-1}=\dfrac{3}{3-1}+\dfrac{3+3}{8}=\dfrac{3}{2}+\dfrac{6}{8}=\dfrac{9}{4}\)
\(b,\) \(dkxd:x\ge0,x\ne1\)
\(A=\dfrac{3}{\sqrt{x}-1}+\dfrac{\sqrt{x}+3}{x-1}\)
\(=\dfrac{3}{\sqrt{x}-1}+\dfrac{\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\left(\sqrt{x}+1\right)+\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\sqrt{x}+3+\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{4\sqrt{x}+6}{x-1}\)
\(B=\dfrac{x+2}{x+\sqrt{x}-2}-\dfrac{\sqrt{x}}{\sqrt{x}+2}\)
\(=\dfrac{\left(x+2\right)\left(\sqrt{x}+2\right)-\sqrt{x}\left(x+\sqrt{x}-2\right)}{\left(x+\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{x\sqrt{x}+2x+2\sqrt{x}+4-x\sqrt{x}-x+2\sqrt{x}}{\left(x+\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{x+4\sqrt{x}+4}{\left(x+\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\left(\sqrt{x}+2\right)^2}{\left(x+\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{(\sqrt{x}+2)^2}{\left(\sqrt{x}+2\right)\left(x+\sqrt{x}-2\right)}\)
\(=\dfrac{\sqrt{x}+2}{x+\sqrt{x}-2}\)
Ta có : \(M=A:B=\dfrac{4\sqrt{x}+6}{x-1}:\dfrac{\sqrt{x}+2}{x+\sqrt{x}-2}\)
\(=\dfrac{4\sqrt{x}+6}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\dfrac{x-\sqrt{x}+2\sqrt{x}-2}{\sqrt{x}+2}\)
\(=\dfrac{4\sqrt{x}+6}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)+2\left(\sqrt{x}-1\right)}{\sqrt{x}+2}\)
\(=\dfrac{4\sqrt{x}+6}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}{\sqrt{x}+2}\)
\(=\dfrac{4\sqrt{x}+6}{\sqrt{x}+1}\)
Vậy \(M=\dfrac{4\sqrt{x}+6}{\sqrt{x}+1}\)
a: KhI x=9 thì A=3/(3-1)=3/2
b: M=A:B
\(=\dfrac{3\sqrt{x}+3+\sqrt{x}+3}{x-1}:\dfrac{x+2-x+\sqrt{x}}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{2\left(2\sqrt{x}+3\right)}{x-1}\cdot\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}{\sqrt{x}+2}=\dfrac{2\left(2\sqrt{x}+3\right)}{\sqrt{x}+1}\)