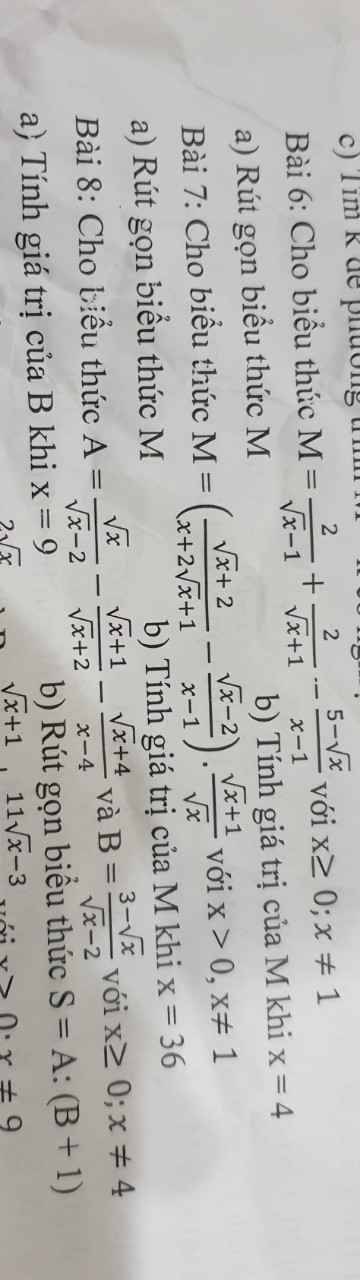Bài 6 :
\(a,\) Rút gọn :
\(M=\dfrac{2}{\sqrt{x}-1}+\dfrac{2}{\sqrt{x}+1}-\dfrac{5-\sqrt{x}}{x-1}\left(dkxd:x\ge0,x\ne1\right)\)
\(=\dfrac{2}{\sqrt{x}-1}+\dfrac{2}{\sqrt{x}+1}-\dfrac{5-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{2\left(\sqrt{x}+1\right)+2\left(\sqrt{x}-1\right)-5+\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{2\sqrt{x}+2+2\sqrt{x}-2-5+\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{5\sqrt{x}-5}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{5\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{5}{\sqrt{x}+1}\)
\(b,\) Khi \(x=4\)
\(\Rightarrow M=\dfrac{5}{\sqrt{4}+1}=\dfrac{5}{2+1}=\dfrac{5}{3}\)
Bài 7 :
\(a,\) Rút gọn :
\(M=\left(\dfrac{\sqrt{x}+2}{x+2\sqrt{x}+1}-\dfrac{\sqrt{x}-2}{x-1}\right).\dfrac{\sqrt{x}+1}{\sqrt{x}}\left(dkxd:x>0,x\ne1\right)\)
\(=\left(\dfrac{\sqrt{x}+2}{\left(\sqrt{x}+1\right)^2}-\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right).\dfrac{\sqrt{x}+1}{\sqrt{x}}\)
\(=\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)-\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\dfrac{\sqrt{x}+1}{\sqrt{x}}\)
\(=\dfrac{x-\sqrt{x}+2\sqrt{x}-2-\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\dfrac{\sqrt{x}+1}{\sqrt{x}}\)
\(=\dfrac{x}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\dfrac{\sqrt{x}+1}{\sqrt{x}}\)
\(=\dfrac{\sqrt{x}^2}{\sqrt{x}-1}.\dfrac{1}{\sqrt{x}}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}-1}\)
\(b,\) Khi \(x=36\)
\(\Rightarrow M=\dfrac{\sqrt{36}}{\sqrt{36}-1}=\dfrac{6}{6-1}=\dfrac{6}{5}\)
8:
a: Khi x=9 thì B=(3-3)/(3-2)=0
b: \(A=\dfrac{x+2\sqrt{x}-x+\sqrt{x}+2-\sqrt{x}-4}{x-4}=\dfrac{2\sqrt{x}-2}{x-4}\)
S=A:(B+1)
\(=\dfrac{2\sqrt{x}-2}{x-4}:\dfrac{1}{\sqrt{x}-2}=\dfrac{2\sqrt{x}-2}{\sqrt{x}+2}\)