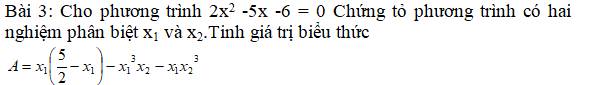Ptr có: `\Delta=(-5)^2-4.2.(-6)=73 > 0`
`=>` Ptr có `2` nghiệm phân biệt
Áp dụng hệ thức Viét có: `{(x_1+x_2=[-b]/a=5/2),(x_1 .x_2=c/a=-3):}`
Ta có: `A=x_1(5/2-x_1)-x_1 ^3 x_2-x_1 x_2 ^3`
`<=>A=x_1(x_1+x_2-x_1)-x_1 .x_2(x_1 ^2 +x_2 ^2)`
`<=>A=x_1 .x_2-x_1 .x_2[(x_1+x_2)^2-2x_1 .x_2]`
`<=>A=-3+3[(5/2)^2-2.(-3)]=135/4`
\(\Delta=25+48=73>0\Rightarrow\) pt có 2 nghiệm pb \(x_1;x_2\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{5}{2}\\x_1x_2=-3\end{matrix}\right.\)
\(A=\dfrac{5}{2}x_1-x_1^2-x_1x_2\left(x_1^2+x_2^2\right)\)
\(=\left(x_1+x_2\right).x_1-x_1^2+3\left(x_1^2+x_2^2\right)\)
\(=x_1x_2+3\left[\left(x_1+x_2\right)^2-2x_1x_2\right]\)
\(=-3+3\left(\dfrac{25}{4}+6\right)=\dfrac{135}{4}\)