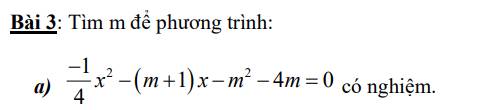Ta có: \(\Delta=b^2-4ac\)
\(=\left[-\left(m+1\right)\right]^2-4.\dfrac{-1}{4}.\left(-m^2-4m\right)\)
\(=m^2+2m+1-m^2-4m\)
\(=-2m+1\)
Để phương trình có nghiệm thì \(\Delta\le0\)
Do đó: \(-2m+1\le0\Leftrightarrow m\ge\dfrac{1}{2}\)
Để pt trên có nghiệm thì \(\Delta>0\)
\(\Delta=b^2-4ac=\left[-\left(m+1\right)\right]^2-4\left(-\dfrac{1}{4}\right)\left(-m^2-4m\right)\)
\(=m+1-m^2-4m\)
\(=-m^2-3m+1\)
\(\Delta>0\Rightarrow-m^2-3m+1>0\)
\(\Rightarrow m>\dfrac{-3+\sqrt{13}}{2}\) và \(m>\dfrac{-3-\sqrt{13}}{2}\) để pt tren có nghiệm