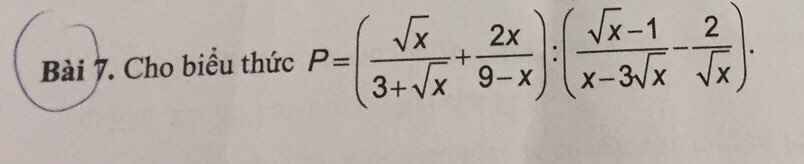Với `x >= 0,x \ne 9` có:
`P=(\sqrt{x}/[3+\sqrt{x}]+[2x]/[9-x]):([\sqrt{x}-1]/[x-3\sqrt{x}]-2/\sqrt{x})`
`P=[\sqrt{x}(\sqrt{x}-3)-2x]/[(\sqrt{x}+3)(\sqrt{x}-3)]:[\sqrt{x}-1-2(\sqrt{x}-3)]/[\sqrt{x}(\sqrt{x}-3)]`
`P=[x-3\sqrt{x}-2x]/[(\sqrt{x}+3)(\sqrt{x}-3)].[\sqrt{x}(\sqrt{x}-3)]/[\sqrt{x}-1-2\sqrt{x}+6]`
`P=[-x-3\sqrt{x}]/[\sqrt{x}+3].\sqrt{x}/[-\sqrt{x}+5]`
`P=x/[\sqrt{x}-5]`
đk x> 0 ;x ≠ 9
\(P=\left(\dfrac{\sqrt{x}\left(3-\sqrt{x}\right)+2x}{9-x}\right):\left(\dfrac{\sqrt{x}-1}{\sqrt{x}\left(\sqrt{x}-3\right)}-\dfrac{2}{\sqrt{x}}\right)\\ =\dfrac{3\sqrt{x}-x+2x}{9-x}:\left(\dfrac{\sqrt{x}-1-2\sqrt{x}+6}{\sqrt{x}\left(\sqrt{x}-3\right)}\right)\\ =\dfrac{3\sqrt{x}-x}{9-x}.\dfrac{5-\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-3\right)}\\ =\dfrac{-\sqrt{x}\left(\sqrt{x}-3\right)}{9-x}.\dfrac{5-\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-3\right)}=\dfrac{\sqrt{x}+5}{9-x}\)