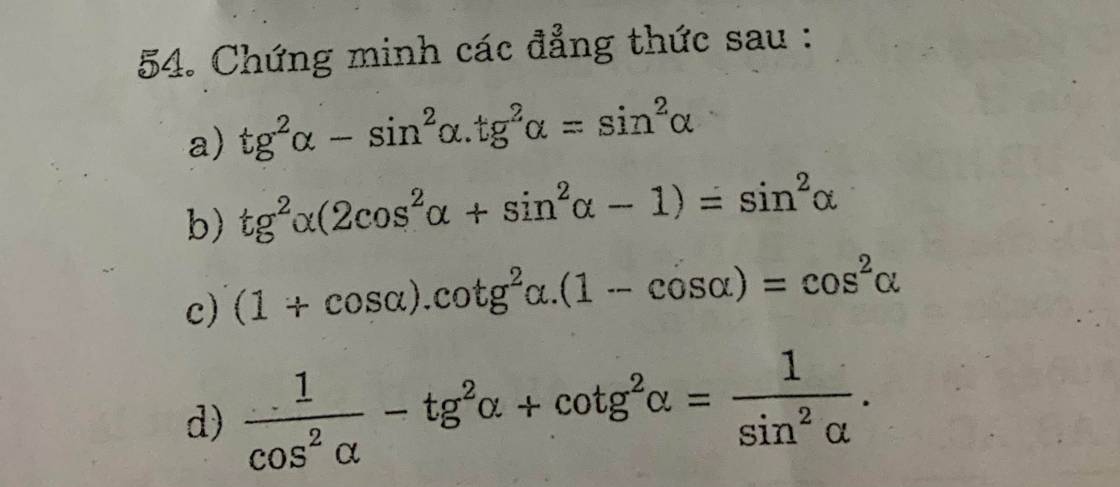\(a,VT=\dfrac{sin^2a}{cos^2a}-sin^2a.\dfrac{sin^2a}{cos^2a}\\ =\dfrac{sin^2a-sin^2a\left(1-cos^2a\right)}{cos^2a}\\ =\dfrac{sin^2a-sin^2a+sin^2a.cos^2a}{cos^2a}\\ =\dfrac{sin^2a.cos^2a}{cos^2a}\\ =sin^2a=VP\)
\(b,=tg^2a\left(2cos^2a+1-cos^2a-1\right)\\ =\dfrac{sin^2a}{cos^2a}.cos^2a\\ =sin^2a=VP\)
\(c,=\left[\left(1+cosa\right)\left(1-cosa\right)\right].\dfrac{cos^2a}{sin^2a}\\ =\left(1-cos^2a\right).\dfrac{cos^2a}{sin^2a}\\ =sin^2a.\dfrac{cos^2a}{sin^2a}\\ =cos^2a=VP\\ d,=\dfrac{1}{cos^2a}-\dfrac{sin^2a}{cos^2a}+\dfrac{cos^2a}{sin^2a}\\ =\dfrac{1-sin^2a}{cos^2a}+\dfrac{cos^2a}{sin^2a}\\ =\dfrac{cos^2a}{cos^2a}+\dfrac{cos^2a}{sin^2a}\\ =1+\dfrac{cos^2a}{sin^2a}\\ =\dfrac{sin^2a+cos^2a}{sin^2a}\\ =\dfrac{1}{sin^2a}=VP\)
`a)VT=tg^2 \alpha(1-sin^2 \alpha)`
`=[sin^2 \alpha]/[cos^2 \alpha].cos^2 \alpha=sin^2 \alpha=VP`
________________________________________________
`b)VT=tg^2 \alpha(2cos^2 \alpha+sin^2 \alpha-1)`
`=tg^2 \alpha(2cos^2 \alpha-cos^2 \alpha)`
`=[sin^2 \alpha]/[cos^2 \alpha].cos^2 \alpha=sin^2 \alpha=VP`
________________________________________________
`c)VT=(1+cos \alpha).cotg^2 \alpha(1-cos \alpha)`
`=(1-cos^2 \alpha).cotg^2 \alpha`
`=sin^2 \alpha.[cos^2 \alpha]/[sin^2 \alpha]=cos^2 \alpha=VP`
_________________________________________________
`d)VT=1/[cos^2 \alpha]-[sin^2 \alpha]/[cos^2 \alpha]+[cos^2 \alpha]/[sin^2 \alpha]`
`=[1-sin^2 \alpha]/[cos^2 \alpha]+[cos^2 \alpha]/[sin^2 \alpha]`
`=[cos^2 \alpha]/[cos^2 \alpha]+[cos^2 \alpha]/[sin^2 \alpha]`
`=1+[cos^2 \alpha]/[sin^2 \alpha]`
`=[sin^2 \alpha+cos^2 \alpha]/[sin^2 \alpha]=1/[sin^2 \alpha]=VP`