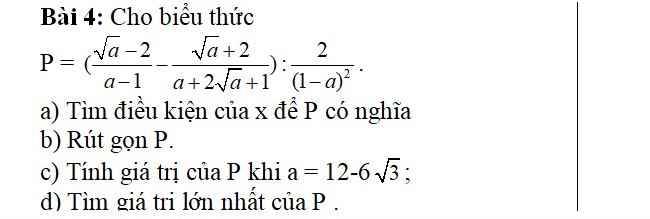a, DKXD: \(\left\{{}\begin{matrix}a\ge0\\a-1\ne0\\a+2\sqrt{a}+1\ne0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}a\ge0\\a\ne1\\\left(\sqrt{a}+1\right)^2\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a\ge0\\a\ne1\end{matrix}\right.\)
b, \(P=\left(\dfrac{\sqrt{a}-2}{a-1}-\dfrac{\sqrt{a}+2}{a+2\sqrt{a}+1}\right):\dfrac{2}{\left(1-a\right)^2}\)
\(=\left(\dfrac{\sqrt{a}-2}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}-\dfrac{\sqrt{a}+2}{\left(\sqrt{a}+1\right)^2}\right).\dfrac{\left(1-a\right)^2}{2}\)
\(=\dfrac{\left(\sqrt{a}-2\right)\left(\sqrt{a}+1\right)-\left(\sqrt{a}+2\right)\left(\sqrt{a}-1\right)}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)^2}.\dfrac{\left(1-a\right)^2}{2}\)
\(=\dfrac{a-2\sqrt{a}+\sqrt{a}-2-\left(a+2\sqrt{a}-\sqrt{a}-2\right)}{\left(a-1\right)\left(\sqrt{a}+1\right)}.\dfrac{\left(a-1\right)^2}{2}\)
\(=\dfrac{-2\sqrt{a}}{\left(a-1\right)\left(\sqrt{a}+1\right)}.\dfrac{\left(a-1\right)^2}{2}\)
\(=\dfrac{-\sqrt{a}\left(a-1\right)}{\left(\sqrt{a}+1\right)}=-\sqrt{a}\left(\sqrt{a}-1\right)\)
c, Khi \(a=12-6\sqrt{3}\) :
\(P=-\sqrt{12-6\sqrt{3}}\left(\sqrt{12-6\sqrt{3}}-1\right)\)
\(=-\left(12-6\sqrt{3}\right)-\sqrt{12-6\sqrt{3}}\)
\(=-\left(12-6\sqrt{3}\right)-\sqrt{\left[\left(\sqrt{3}\right)^2-2.\sqrt{3}.3+3^2\right]}\)
\(=-\left(12-6\sqrt{3}\right)-\sqrt{\left(\sqrt{3}-3\right)^2}\)
\(=-\left(12-6\sqrt{3}\right)-\left|\sqrt{3}-3\right|\)
\(=-12+6\sqrt{3}-\left[-\left(\sqrt{3}-3\right)\right]\)
\(=-12+6\sqrt{3}+\sqrt{3}-3\)
\(=-15+7\sqrt{3}\)
a: ĐKXĐ: a>=0; a<>1
b: \(P=\dfrac{a-\sqrt{a}-2-a-\sqrt{a}+2}{\left(\sqrt{a}+1\right)^2\cdot\left(\sqrt{a}-1\right)}\cdot\dfrac{\left(a-1\right)^2}{2}\)
\(=-\sqrt{a}\left(\sqrt{a}-1\right)\)
c: Khi \(a=12-6\sqrt{3}=\left(3-\sqrt{3}\right)^2\) thì
\(P=-\left(3-\sqrt{3}\right)\left(3-\sqrt{3}-1\right)\)
\(=\left(\sqrt{3}-3\right)\left(2-\sqrt{3}\right)\)
\(=2\sqrt{3}-3-6+3\sqrt{3}=5\sqrt{3}-9\)