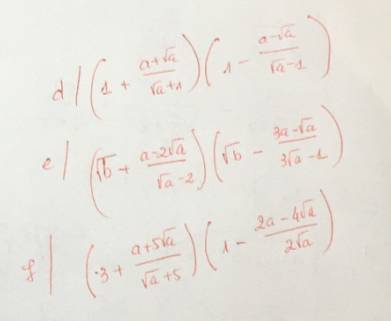d: \(=\left(1+\sqrt{a}\right)\left(1-\sqrt{a}\right)=1-a\)
e: \(=\left(\sqrt{b}+\sqrt{a}\right)\cdot\left(\sqrt{b}-\sqrt{a}\right)=b-a\)
f: \(=\left(3+\sqrt{a}\right)\left(1-\dfrac{2\sqrt{a}\left(a-2\right)}{2\sqrt{a}}\right)\)
\(=\left(3+\sqrt{a}\right)\left(1-a+2\right)\)
\(=\left(\sqrt{a}+3\right)\left(3-a\right)\)
\(=3\sqrt{a}-a\sqrt{a}+9-3a\)
d.
\(=\left(1+\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)}{\sqrt{a}+1}\right)\left(1-\dfrac{\sqrt{a}\left(\sqrt{a}-1\right)}{\sqrt{a}-1}\right)\)
\(=\left(1+\sqrt{a}\right)\left(1-\sqrt{a}\right)=1-a\)
e.
\(=\left(\sqrt{b}+\dfrac{\sqrt{a}\left(\sqrt{a}-2\right)}{\sqrt{a}-2}\right)\left(\sqrt{b}-\dfrac{\sqrt{a}\left(3\sqrt{a}-1\right)}{3\sqrt{a}-1}\right)\)
\(=\left(\sqrt{b}+\sqrt{a}\right)\left(\sqrt{b}-\sqrt{a}\right)=b-a\)
f.
\(=\left(3+\dfrac{\sqrt{a}\left(\sqrt{a}+5\right)}{\sqrt{a}+5}\right)\left(1-\dfrac{2\sqrt{a}\left(\sqrt{a}-2\right)}{2\sqrt{a}}\right)\)
\(=\left(3+\sqrt{a}\right)\left(1-\left(\sqrt{a}-2\right)\right)=\left(3+\sqrt{a}\right)\left(3-\sqrt{a}\right)\)
\(=9-a\)