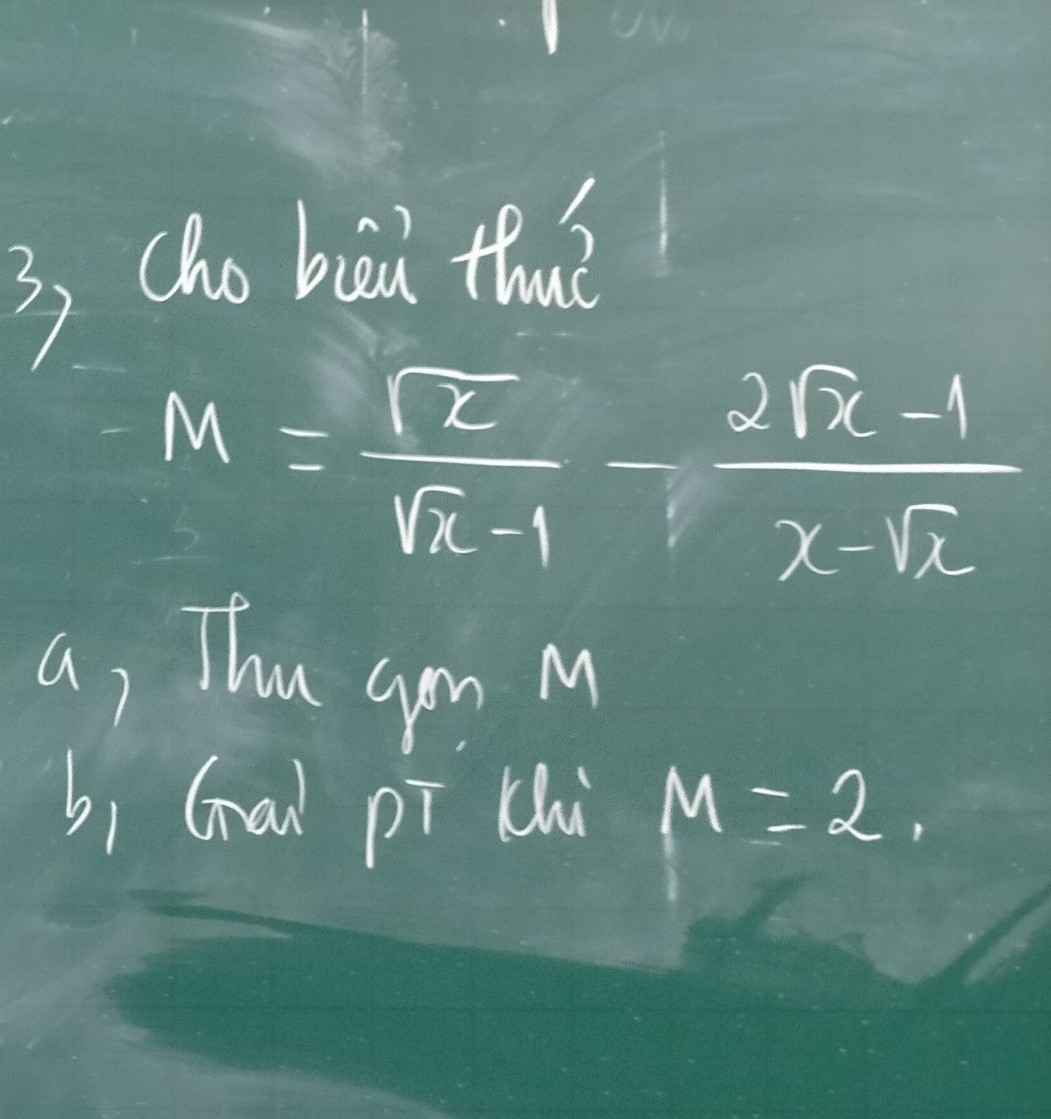Question

Answer 1

a: \(M=\dfrac{x-2\sqrt{x}+1}{x-\sqrt{x}}=\dfrac{\sqrt{x}-1}{\sqrt{x}}\)

b: Để M=2 thì \(2\sqrt{x}=\sqrt{x}-1\)

=>căn x=-1(vô lý)

Answer 2

đk x> 0 ; x ≠ 1

\(a,M=\dfrac{\sqrt{x}.\sqrt{x}-2\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}\\ =\dfrac{x-2\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}\\ =\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}\left(\sqrt{x}-1\right)}\\ =\dfrac{\sqrt{x}-1}{\sqrt{x}}\\ b,M=2\\ \dfrac{\sqrt{x}-1}{\sqrt{x}}=2\\ \sqrt{x}-1=2\sqrt{x}\\ \sqrt{x}-2\sqrt{x}-1=0\\ -\sqrt{x}-1=0\\ -\sqrt{x}=1\left(voli\right)=>\varnothing\)