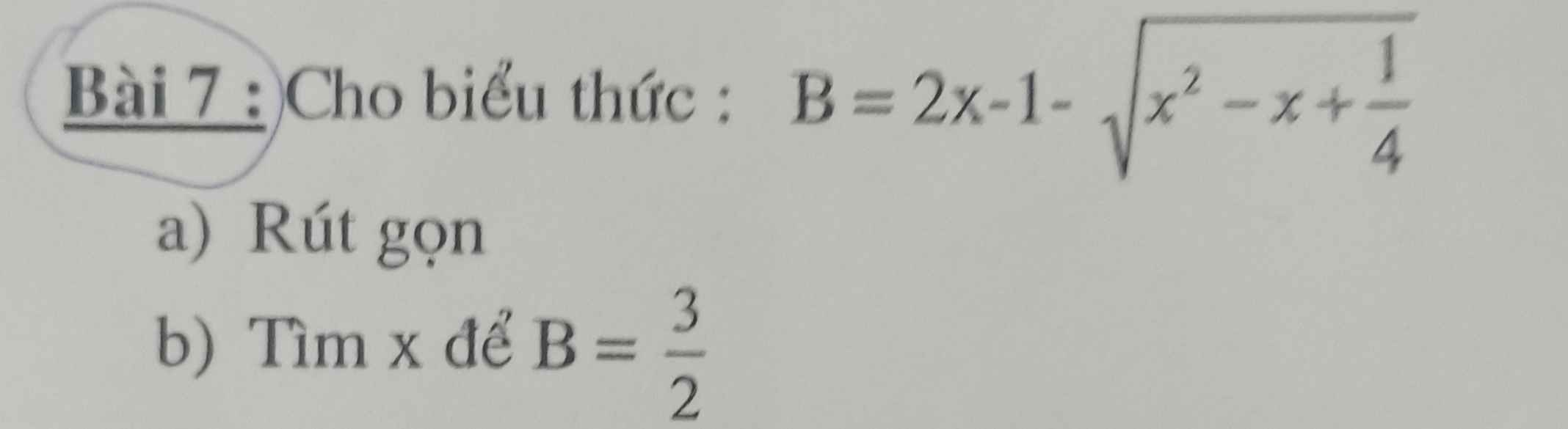Question

Answer 1

`a)B = 2x-1 - sqrt{x^2 -x+1/4}`

`B=2x-1 - sqrt{ x^2 - 2.x*1/2 + (1/2)^2}`

`B = 2x-1 - sqrt{(x-1/2)^2 }`

`B = 2x-1- |x-1/2|`

`=>text{ ta có hai trường hợp}`

`@TH1 : x >=1/2`

`=> B = 2x-1-(x-1/2) = 2x-1-x+1/2 = x-1/2`

`@TH2 : x<1/2`

`=> B = 2x-1-(1/2-x) = 2x-1-1/2 +x = 3x-3/2 = 3(x-1/2)`

`b) @TH1 : B=x-1/2 =3/2 (x>=1/2)`

`<=> x=3/2 +1/2 =4/2 =2`

`@TH2 : B=3(x-1/2) = 3/2 (x<1/2)`

`<=> x-1/2 = 3/2 * 1/3 =1/2`

`=> x = 1/2 +1/2 =2/2 =1`

Answer 2

a: \(B=2x-1-\left|x-\dfrac{1}{2}\right|\)

TH1: x>=1/2

\(B=2x-1-x+\dfrac{1}{2}=x-\dfrac{1}{2}\)

TH2: x<1/2

\(B=2x-1+x-\dfrac{1}{2}=3x-\dfrac{3}{2}\)

b: TH1: x>=1/2

=>x-1/2=3/2

hay x=2(nhận)

TH2: x<1/2

=>3x-3/2=3/2

=>x=3(loại)