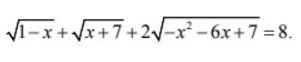`ĐK: -7 <= x <= 1`
Đặt `\sqrt{1-x}+\sqrt{x+7}=t` `(t >= 0)`
`<=>1-x+x+7+2\sqrt{(1-x)(x+7)}=t^2`
`<=>8+2\sqrt{-x^2-6x+7}=t^2`
`<=>2\sqrt{-x^2-6x+7}=t^2-8`
Khi đó ptr có dạng:
`t+t^2-8=8`
`<=>t^2+t-16=0`
Ptr có:`\Delta=1^2-4.(-16)=65 > 0`
`=>` Ptr có `2` nghiệm pb
`t_1=[-b+\sqrt{\Delta}]/[2a]=[-1+\sqrt{65}]/2` (t/m)
`t_2=[-b-\sqrt{\Delta}]/[2a]=[-1-\sqrt{65}]/2` (ko t/m)
`@t=[-1+\sqrt{65}]/2=>\sqrt{1-x}+\sqrt{x+7}=[-1+\sqrt{65}]/2`
`<=>1-x+x+7+2\sqrt{-x^2-6x+7}=[33-\sqrt{65}]/2`
`<=>\sqrt{-x^2-6x+7}=[17-\sqrt{65}]/4`
`<=>-x^2-6x+7=[354-34\sqrt{65}]/16`
`<=>x^2+6x+[242-34\sqrt{65}]/16=0`
Ptr có:`\Delta'=3^2-[242-34\sqrt{65}]/16=[34\sqrt{65}-98]/16 > 0`
`=>`Ptr có `2` nghiệm pb
`x_1=[-b'+\sqrt{\Delta'}]/a=-3+[\sqrt{34\sqrt{65}-98]/4=[-12+\sqrt{34\sqrt{65}-98}]/4`
`x_2=[-b'-\sqrt{\Delta'}]/a=-3-[\sqrt{34\sqrt{65}-98]/4=[-12-\sqrt{34\sqrt{65}-98}]/4`
Vậy `S={[-12+-\sqrt{34\sqrt{65}-98}]/4}`
Số ra khủng khiếp qué :)