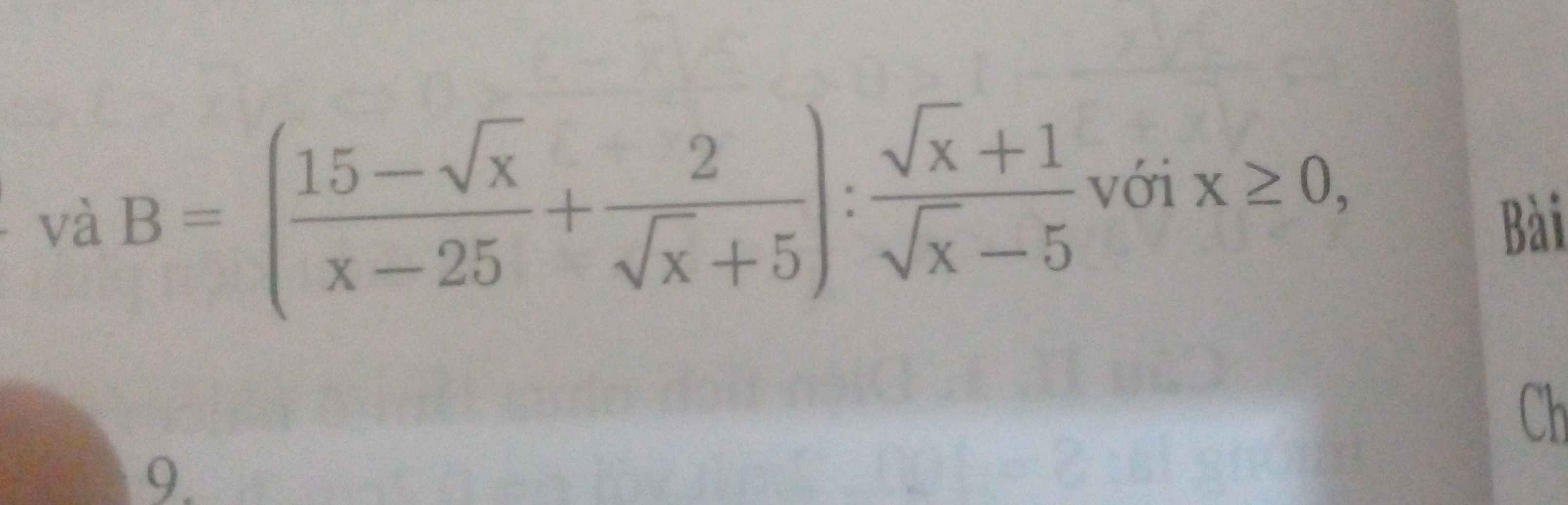Question

Answer 1

Giúp mik bài này nhanh đc ko ạ

 

Answer 2

\(B=\dfrac{15-\sqrt{x}+2\sqrt{x}-10}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}\cdot\dfrac{\sqrt{x}-5}{\sqrt{x}+1}=\dfrac{1}{\sqrt{x}+1}\)

Answer 3

\(B=\left(\dfrac{15-\sqrt{x}}{x-25}+\dfrac{2}{\sqrt{x}+5}\right):\dfrac{\sqrt{x}+1}{\sqrt{x}-5}\);\(x\ge0;x\ne25\)

\(B=\left(\dfrac{15-\sqrt{x}+2\left(\sqrt{x}-5\right)}{\left(\sqrt{x}-5\right)\left(\sqrt{x}+5\right)}\right):\dfrac{\sqrt{x}+1}{\sqrt{x}-5}\)

\(B=\left(\dfrac{15-\sqrt{x}+2\sqrt{x}-10}{\left(\sqrt{x}-5\right)\left(\sqrt{x}+5\right)}\right).\dfrac{\sqrt{x}-5}{\sqrt{x}+1}\)

\(B=\dfrac{\left(5+\sqrt{x}\right)\left(\sqrt{x}-5\right)}{\left(\sqrt{x}-5\right)\left(\sqrt{x}+5\right)\left(\sqrt{x}+1\right)}\)

\(B=\dfrac{1}{\sqrt{x}+1}\)