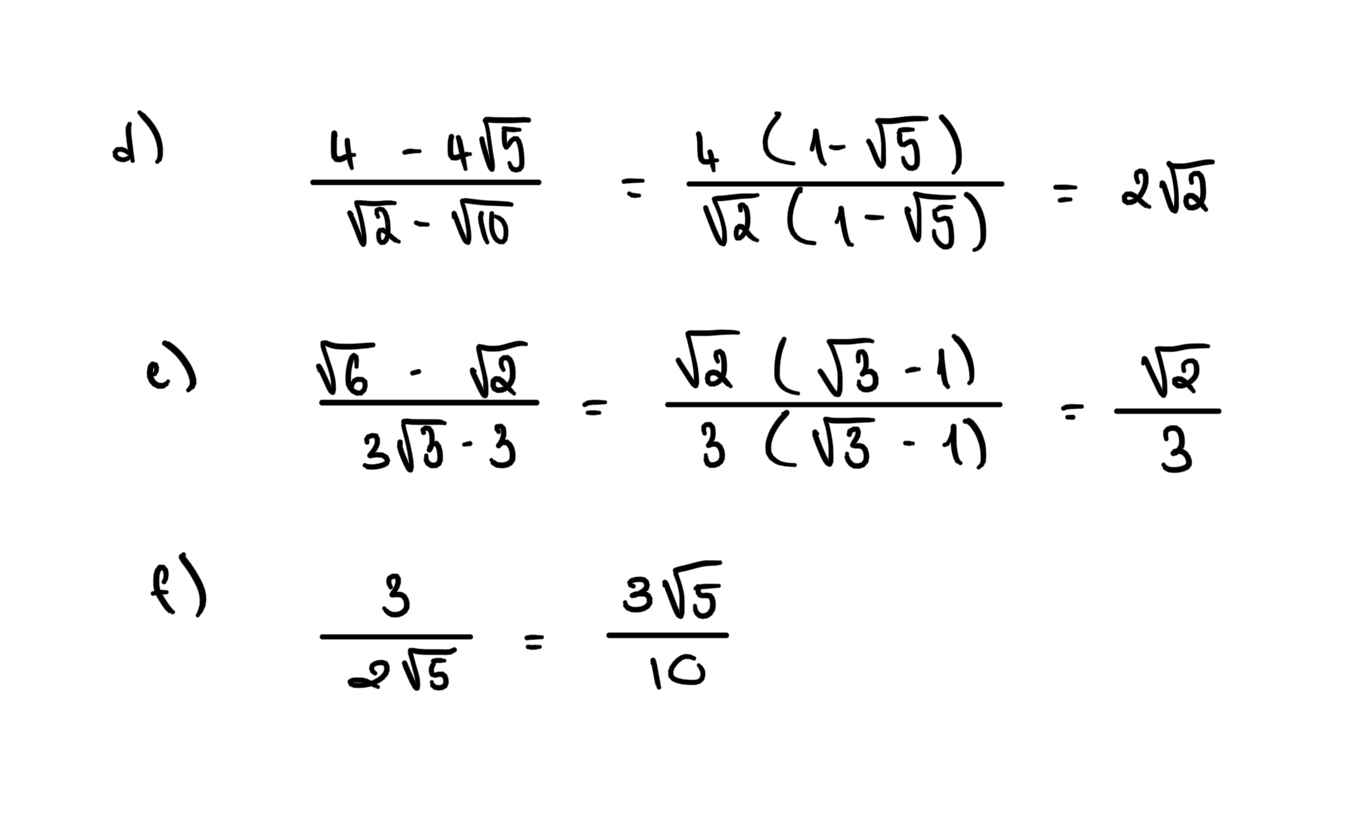f: \(=\dfrac{6\sqrt{5}}{20}=\dfrac{3\sqrt{5}}{10}\)
\(d,=\dfrac{4\left(1-\sqrt{5}\right)}{\sqrt{2}\left(1-\sqrt{5}\right)}=2\sqrt{2}\\ e,=\dfrac{\sqrt{2}\left(\sqrt{3}-1\right)}{3\left(\sqrt{3}-1\right)}=\dfrac{\sqrt{2}}{3}\\ f,=\dfrac{3\cdot2\sqrt{5}}{2^2\cdot5}=\dfrac{6\sqrt{5}}{20}=\dfrac{3\sqrt{5}}{10}\)
`d. \frac{4-4sqrt5}{sqrt2-sqrt10}=\frac{4(1-sqrt5)}{sqrt2(1-sqrt5)}=4/sqrt2`
`e. \frac{sqrt6-sqrt2}{3sqrt3-3}=\frac{sqrt2(sqrt3-1)}{3(sqrt3-1)}=sqrt2/3`
`f. \frac{3}{2sqrt5}=\frac{3sqrt5}{2.5}=\frac{3sqrt5}{10}`