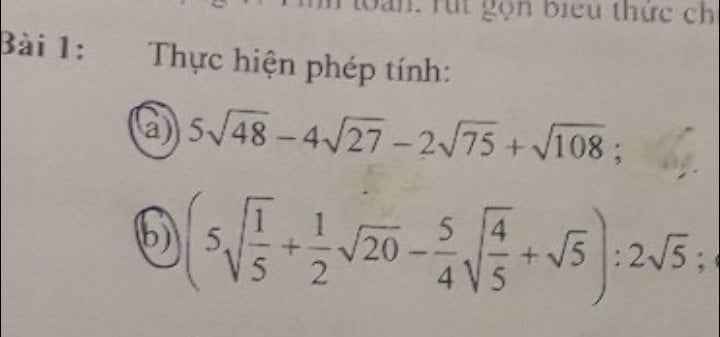a: \(=20\sqrt{3}-12\sqrt{3}-10\sqrt{3}+6\sqrt{3}=4\sqrt{3}\)
a/ \(5\sqrt{48}-4\sqrt{27}-2\sqrt{75}+\sqrt{108}\)
\(=20\sqrt{3}-12\sqrt{3}-10\sqrt{3}+6\sqrt{3}\)
\(=4\sqrt{3}\)
b/ \(\left(5\sqrt{\dfrac{1}{5}}+\dfrac{1}{2}\sqrt{20}-\dfrac{5}{4}\sqrt{\dfrac{4}{5}}+\sqrt{5}\right):2\sqrt{5}\)
\(=\left(\sqrt{5}+\sqrt{5}-\dfrac{1}{2}\sqrt{5}+\sqrt{5}\right):2\sqrt{5}\)
\(=\dfrac{5}{2}\sqrt{5}:2\sqrt{5}\)
\(=\dfrac{5}{4}\sqrt{5}\)
b) (5\(\sqrt{\dfrac{1}{5}}\)+\(\dfrac{1}{2}\sqrt{20}-\dfrac{5}{4}\)\(\sqrt{\dfrac{4}{5}}+\sqrt{5}\) ) :2\(\sqrt{5}\)
=(\(\sqrt{5}+\)\(\sqrt{5}\) -\(\dfrac{\sqrt{5}}{2}\)+\(\sqrt{5}\)):2\(\sqrt{5}\)
=0,5+0,5-0,25+0,5
=1,25
\(\left(\sqrt{5}+\sqrt{5}-\dfrac{1}{2}\sqrt{5}\right)\div2\sqrt{5}=\dfrac{3}{2}\sqrt{5}\div2\sqrt{5}=\dfrac{3}{4}\)