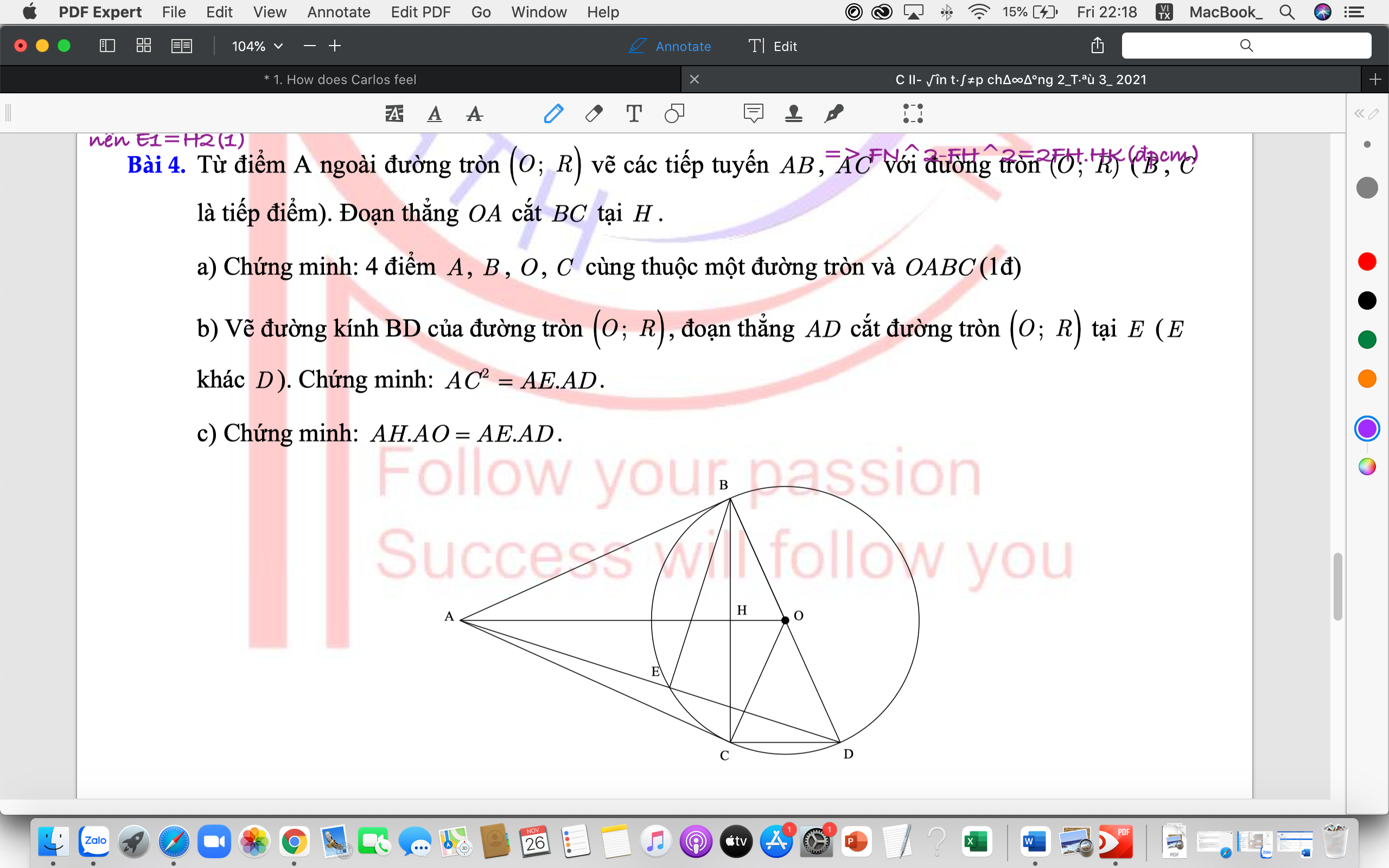
\(a,\widehat{ABO}+\widehat{ACO}=90^0+90^0=180^0\) nên ABOC nt hay A,B,O,C cùng thuộc 1 đt
\(b,\) Theo tc tiếp tuyến cắt dây cung: \(\widehat{ACE}=\dfrac{1}{2}sđ\stackrel\frown{EC}\)
Lại có \(\widehat{CDA}=\dfrac{1}{2}sđ\stackrel\frown{EC}\) (góc nt)
\(\Rightarrow\widehat{ACE}=\widehat{CDA}\\ \Rightarrow\Delta ACE\sim\Delta ADC\left(g.g\right)\\ \Rightarrow\dfrac{AC}{AD}=\dfrac{AE}{AC}\\ \Rightarrow AC^2=AE\cdot AD\)
\(c,\) Theo tc 2 tiếp tuyến cắt nhau: \(AC=AB\Rightarrow A\in\text{ trung trực }BC\)
Lại có \(OB=OC=R\Rightarrow O\in\text{ trung trực BC}\)
\(\Rightarrow OA\text{ là trung trực }BC\\ \Rightarrow OA\perp BC\text{ tại H}\\ \text{Áp dụng HTL: }AC^2=AH\cdot AO\\ \text{Mà }AC^2=AE\cdot AD\\ \Rightarrow AH\cdot AO=AE\cdot AD\)