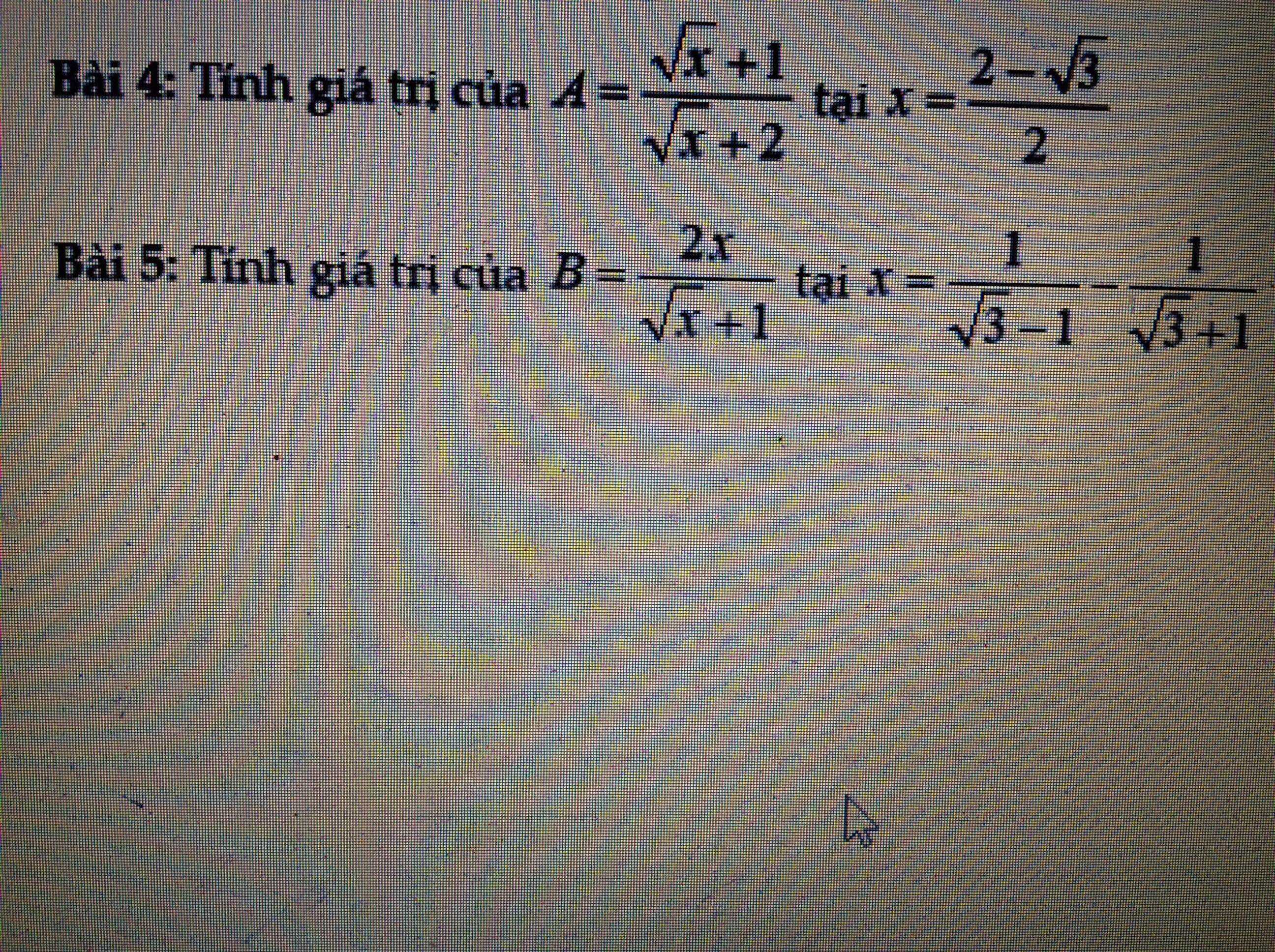Bài 4:
\(x=\dfrac{2-\sqrt{3}}{2}\Leftrightarrow\sqrt{x}=\sqrt{\dfrac{2-\sqrt{3}}{2}}=\dfrac{\sqrt{4-2\sqrt{3}}}{2}=\dfrac{\sqrt{\left(\sqrt{3}-1\right)^2}}{2}=\dfrac{\sqrt{3}-1}{2}\)
\(A=\dfrac{\sqrt{x}+1}{\sqrt{x}+2}=\dfrac{\dfrac{\sqrt{3}-1}{2}+1}{\dfrac{\sqrt{3}-1}{2}+2}=\dfrac{\sqrt{3}+1}{2}:\dfrac{\sqrt{3}+3}{2}\)
\(=\dfrac{\sqrt{3}+1}{2}.\dfrac{2}{\sqrt{3}+3}=\dfrac{\sqrt{3}+1}{\sqrt{3}+3}\)
Bài 5:
\(x=\dfrac{\sqrt{3}+1-\sqrt{3}+1}{3-1}=\dfrac{2}{2}=1\)
\(B=\dfrac{2x}{\sqrt{x}+1}=\dfrac{2.1}{1+1}=\dfrac{2}{2}=1\)
Bài 4:
\(A=\dfrac{\dfrac{2-\sqrt{3}}{2}+1}{\dfrac{2-\sqrt{3}}{2}+2}=\dfrac{\dfrac{2-\sqrt{3}+2}{2}}{\dfrac{2-\sqrt{3}+4}{2}}=\dfrac{4-\sqrt{3}}{2}\cdot\dfrac{2}{6-\sqrt{3}}\\ A=\dfrac{4-\sqrt{3}}{6-\sqrt{3}}=\dfrac{\left(4-\sqrt{3}\right)\left(6+\sqrt{3}\right)}{33}=\dfrac{21-2\sqrt{3}}{33}\)
Bài 5:
\(x=\dfrac{1}{\sqrt{3}-1}-\dfrac{1}{\sqrt{3}+1}=\dfrac{\sqrt{3}+1-\sqrt{3}+1}{\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)}=\dfrac{2}{2}=1\\ \Leftrightarrow B=\dfrac{2\cdot1}{1+1}=\dfrac{2}{2}=1\)
Bài 4:
\(\sqrt{x}=\sqrt{\dfrac{2-\sqrt{3}}{2}}=\sqrt{\dfrac{4-2\sqrt{3}}{4}}=\dfrac{\sqrt{3}-1}{2}\)
\(A=\dfrac{\dfrac{\sqrt{3}-1}{2}+1}{\dfrac{\sqrt{3}-1}{2}+2}=\dfrac{\sqrt{3}+1}{2}:\dfrac{\sqrt{3}+3}{2}\\ A=\dfrac{\sqrt{3}+1}{\sqrt{3}+3}=\dfrac{\left(\sqrt{3}+1\right)\left(3-\sqrt{3}\right)}{6}=\dfrac{2\sqrt{3}}{6}=\dfrac{\sqrt{3}}{3}\)