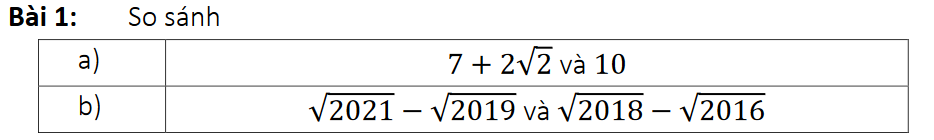a: \(10=7+3\)
mà \(3>2\sqrt{2}\)
nên \(7+2\sqrt{2}< 10\)
Lời giải:
a. $7+2\sqrt{2}=7+\sqrt{8}<7+\sqrt{9}=7+3=10$
b.
$\sqrt{2021}-\sqrt{2019}=\frac{2021-2019}{\sqrt{2021}+\sqrt{2019}}=\frac{2}{\sqrt{2021}+\sqrt{2019}}$
$\sqrt{2018}-\sqrt{2016}=\frac{2018-2016}{\sqrt{2018}+\sqrt{2016}}$
$=\frac{2}{\sqrt{2018}+\sqrt{2016}}$
Dễ thấy $\frac{2}{\sqrt{2021}+\sqrt{2019}}< \frac{2}{\sqrt{2018}+\sqrt{2016}}$ do $\sqrt{2021}+\sqrt{2019}> \sqrt{2018}+\sqrt{2016}$
Do đó:
$\sqrt{2021}-\sqrt{2019}< \sqrt{2018}-\sqrt{2016}$