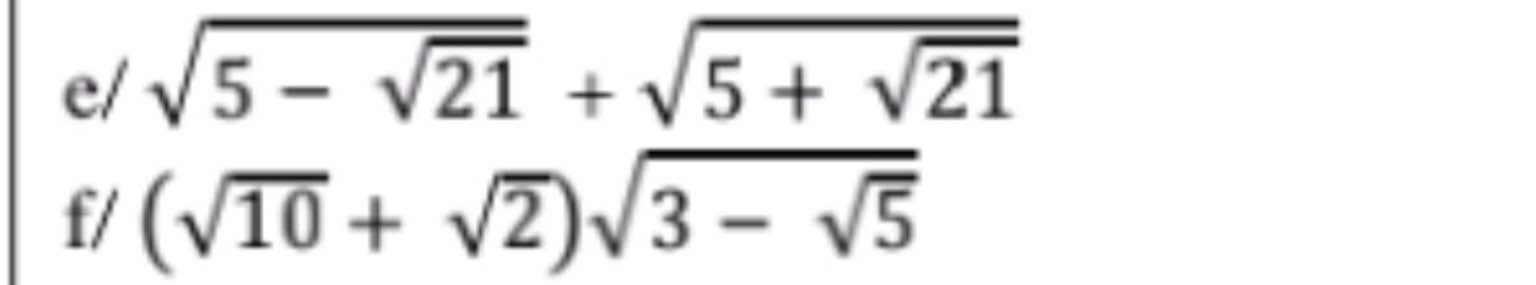Question

Answer 1

f: Ta có: \(\left(\sqrt{10}+\sqrt{2}\right)\cdot\sqrt{3-\sqrt{5}}\)

\(=\left(\sqrt{5}+1\right)\left(\sqrt{5}-1\right)\)

=5-1

=4

Answer 2

e) \(\sqrt{5-\sqrt{21}}+\sqrt{5+\sqrt{21}}\\ =\sqrt{\dfrac{1}{2}\left(10-2\sqrt{21}\right)}+\sqrt{\dfrac{1}{2}\left(10+2\sqrt{21}\right)}\\ =\dfrac{\sqrt{10-2\sqrt{21}}}{\sqrt{2}}+\dfrac{\sqrt{10+2\sqrt{21}}}{\sqrt{2}}\\ =\dfrac{\sqrt{7-2\sqrt{3}.\sqrt{7}+3}+\sqrt{7+2\sqrt{3}.\sqrt{7}+3}}{\sqrt{2}}\\ =\dfrac{\sqrt{7}-\sqrt{3}+\sqrt{7}+\sqrt{3}}{\sqrt{2}}\\ =\dfrac{\sqrt{7}}{\sqrt{2}}\)