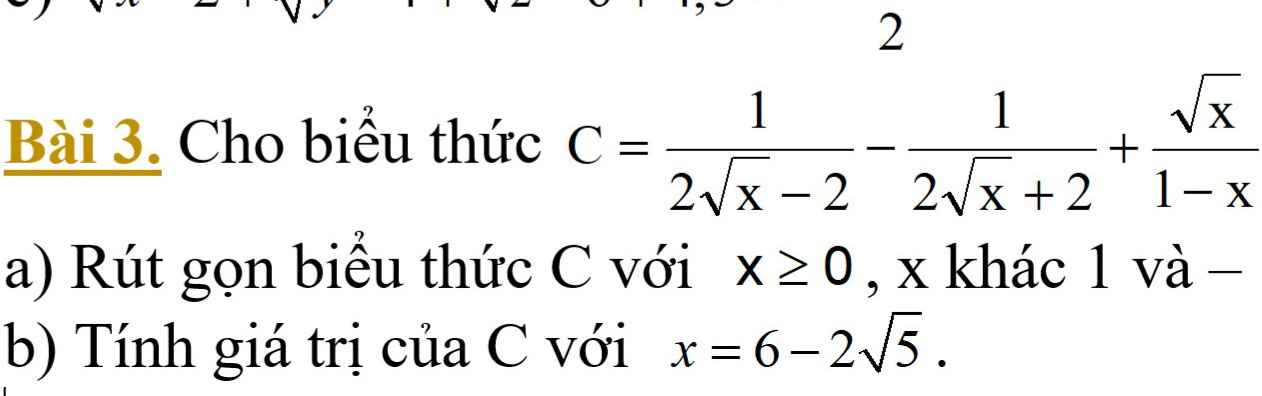a) \(C=\dfrac{1}{2\sqrt{x}-2}-\dfrac{1}{2\sqrt{x}+2}+\dfrac{\sqrt{x}}{1-x}\left(đk:x\ge0,x\ne1\right)\)
\(=\dfrac{2\sqrt{x}+2-2\sqrt{x}+2-4\sqrt{x}}{4x-4}=\dfrac{4-4\sqrt{x}}{4x-4}=\dfrac{1-\sqrt{x}}{x-1}=-\dfrac{1}{1+\sqrt{x}}\)
b) \(C=-\dfrac{1}{1+\sqrt{x}}=\dfrac{-1}{1+\sqrt{6-2\sqrt{5}}}=\dfrac{-1}{1+\sqrt{\left(\sqrt[]{5}-1\right)^2}}=\dfrac{-1}{1+\sqrt{5}-1}=\dfrac{-1}{\sqrt{5}}=-\dfrac{\sqrt{5}}{5}\)
a: Ta có: \(C=\dfrac{1}{2\sqrt{x}-2}-\dfrac{1}{2\sqrt{x}+2}-\dfrac{\sqrt{x}}{x-1}\)
\(=\dfrac{\sqrt{x}+1-\sqrt{x}+1-2\sqrt{x}}{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{-2\left(\sqrt{x}-1\right)}{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=-\dfrac{1}{\sqrt{x}+1}\)