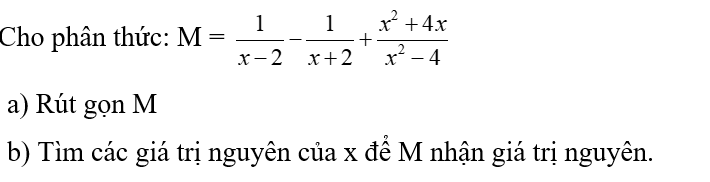\(a,M=\dfrac{1}{x-2}-\dfrac{1}{x+2}+\dfrac{x^2+4x}{x^2-4}\left(x\ne2;x\ne-2\right)\\ M=\dfrac{x+2-x+2+x^2+4x}{\left(x-2\right)\left(x+2\right)}\\ M=\dfrac{\left(x+2\right)^2}{\left(x-2\right)\left(x+2\right)}=\dfrac{x+2}{x-2}\)
\(b,M=\dfrac{x+2}{x-2}=\dfrac{x-2+4}{x-2}=1+\dfrac{4}{x-2}\)
Để \(M\in Z\Leftrightarrow\dfrac{4}{x-2}\in Z\Leftrightarrow x-2\inƯ\left(4\right)=\left\{-4;-2;-1;1;2;4\right\}\)
\(\Leftrightarrow x\in\left\{-2;0;1;3;4;6\right\}\)
Mà \(x\ne2;x\ne-2\)
Vậy \(x\in\left\{0;1;3;4;6\right\}\) thì M nguyên
\(đkxđ:x\ne\pm2\)
\(a,M=\dfrac{x+4}{x-4}\)
b, để M nguyên thì
\(x+4⋮x-4\\ \Rightarrow8⋮x-4\\ \Rightarrow x-4\in\left\{-8;-4;-2;-1;1;2;4;8\right\}\\ \Rightarrow x\in\left\{-4;0;2;3;5;6;8;12\right\}\)
mà x khác 2 nên \(x\in\left\{-4;0;3;5;6;8;12\right\}\)
tik mik nha
a: Ta có: \(M=\dfrac{1}{x-2}-\dfrac{1}{x+2}+\dfrac{x^2+4x}{x^2-4}\)
\(=\dfrac{x+2-x+2+x^2+4x}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x^2+4x+4}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x+2}{x-2}\)
b: Để M nguyên thì \(x+2⋮x-2\)
\(\Leftrightarrow4⋮x-2\)
\(\Leftrightarrow x-2\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow x\in\left\{3;1;4;0;6;-2\right\}\)
Kết hợp ĐKXĐ, ta được: \(x\in\left\{3;1;4;0;6\right\}\)