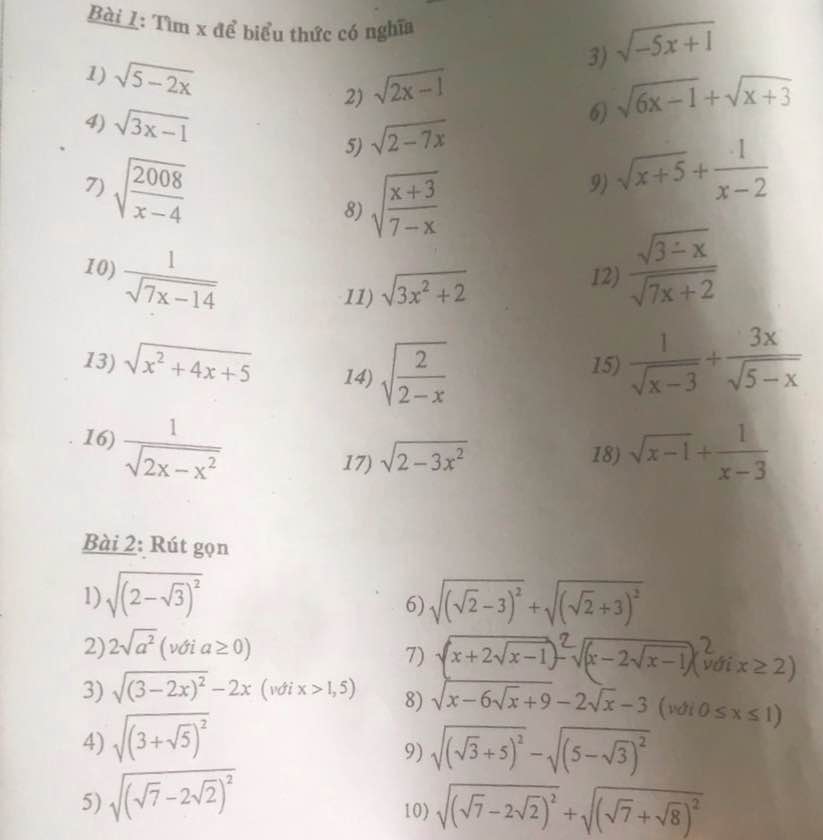Bài 2:
1: \(\sqrt{\left(2-\sqrt{3}\right)^2}\)
\(=\left|2-\sqrt{3}\right|\)
\(=2-\sqrt{3}\)
2: \(2\sqrt{a^2}\)
\(=2\left|a\right|\)
=2a
3: \(\sqrt{\left(3-2x\right)^2}-2x\)
\(=2x-3-2x\)
=-3
4: \(\sqrt{\left(3+\sqrt{5}\right)^2}\)
\(=\left|3+\sqrt{5}\right|\)
\(=3+\sqrt{5}\)
5: \(\sqrt{\left(\sqrt{7}-2\sqrt{2}\right)^2}\)
\(=\left|\sqrt{7}-2\sqrt{2}\right|\)
\(=2\sqrt{2}-\sqrt{7}\)
Bài 1:
1) Để \(\sqrt{5-2x}\) có nghĩa thì \(5-2x\ge0\Leftrightarrow x\le\dfrac{5}{2}\)
2) Để \(\sqrt{2x-1}\) có nghĩa thì \(2x-1\ge0\Leftrightarrow x\ge\dfrac{1}{2}\)
3) Để \(\sqrt{-5x+1}\) có nghĩa thì \(-5x+1\ge0\Leftrightarrow x\le\dfrac{1}{5}\)
4) Để \(\sqrt{3x-1}\) có nghĩa thì \(3x-1\ge0\Leftrightarrow x\ge\dfrac{1}{3}\)
5) Để \(\sqrt{2-7x}\) có nghĩa thì \(2-7x\ge0\Leftrightarrow x\le\dfrac{2}{7}\)
6) Để \(\sqrt{6x-1}+\sqrt{x+3}\) có nghĩa thì \(\left\{{}\begin{matrix}6x-1\ge0\\x+3\ge0\end{matrix}\right.\Leftrightarrow x\ge\dfrac{1}{6}\)
7) Để \(\sqrt{\dfrac{2008}{x-4}}\) có nghĩa thì \(\dfrac{2008}{x-4}\ge0\Leftrightarrow x-4\ge0\Leftrightarrow x\ge4\)