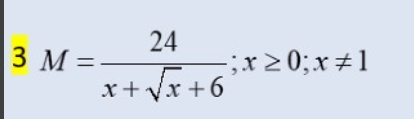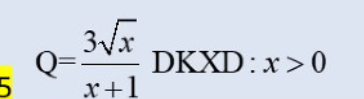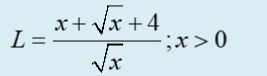1.
\(M=\dfrac{24}{x+\sqrt{x}+6}\)
\(\Leftrightarrow Mx+M\sqrt{x}+6M=24\)
\(\Leftrightarrow Mx+M\sqrt{x}+6M-24=0\)
\(\Delta=M^2-4M\left(6M-24\right)=-23M^2+96M\ge0\)
\(\Leftrightarrow0\le x\le\dfrac{96}{23}\)
\(M_{min}=0\Rightarrow\) Không tồn tại x thỏa mãn để M đạt GTNN bằng 0.
\(M_{max}=\dfrac{96}{23}\Leftrightarrow\dfrac{24}{x+\sqrt{x}+6}=\dfrac{96}{23}\Leftrightarrow...\)
2.
\(Q=\dfrac{3\sqrt{x}}{x+1}\le\dfrac{3\sqrt{x}}{2\sqrt{x}}=\dfrac{3}{2}\)
\(\Rightarrow Q_{max}=\dfrac{3}{2}\Leftrightarrow x=1\)
3.
\(L=\dfrac{x+\sqrt{x}+4}{\sqrt{x}}=\sqrt{x}+\dfrac{4}{\sqrt{x}}+1\ge4+1=5\)
\(\Rightarrow L_{min}=5\Leftrightarrow x=4\)