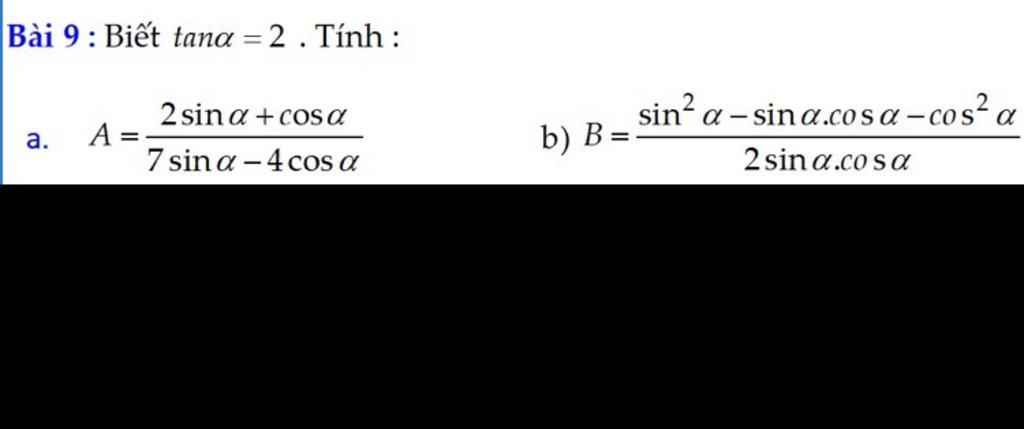a. Chia cả tử và mẫu cho \(cosa\)
\(A=\dfrac{\dfrac{2sina}{cosa}+\dfrac{cosa}{cosa}}{\dfrac{7sina}{cosa}-\dfrac{4cosa}{cosa}}=\dfrac{2tana+1}{7tana-4}=\dfrac{2.2+1}{7.2-4}=...\)
b. Chia cả tử và mẫu cho \(cos^2a\)
\(B=\dfrac{\dfrac{sin^2a}{cos^2a}-\dfrac{sina.cosa}{cos^2a}-\dfrac{cos^2a}{cos^2a}}{\dfrac{2sina.cosa}{cos^2a}}=\dfrac{tan^2a-tana-1}{2tana}=\dfrac{2^2-2-1}{2.2}=...\)
\(tana=2\Rightarrow sina=2cosa\)
a, \(A=\dfrac{2sina+cosa}{7sina-4cosa}\)
\(=\dfrac{4cosa+cosa}{14cosa-4cosa}\)
\(=\dfrac{5cosa}{10cosa}=\dfrac{1}{2}\)
b, \(B=\dfrac{sin^2a-sina.cosa-cos^2a}{2sina.cosa}\)
\(=\dfrac{4cos^2a-2cos^2a-cos^2a}{4cos^2a}\)
\(=\dfrac{cos^2a}{4cos^2a}=\dfrac{1}{4}\)
Vì tan a=2=sina/cosa
=>sina=2cos a
a.A=2sina+cosa/7sina-4cosa
=4cosa+cosa/14cosa-4cosa
=5cosa/10cosa=1/2
b.B=4cos^2a-2cos^2a-cos^2a/4cos^2a
=cos^2a/4cos^2a
=1/4