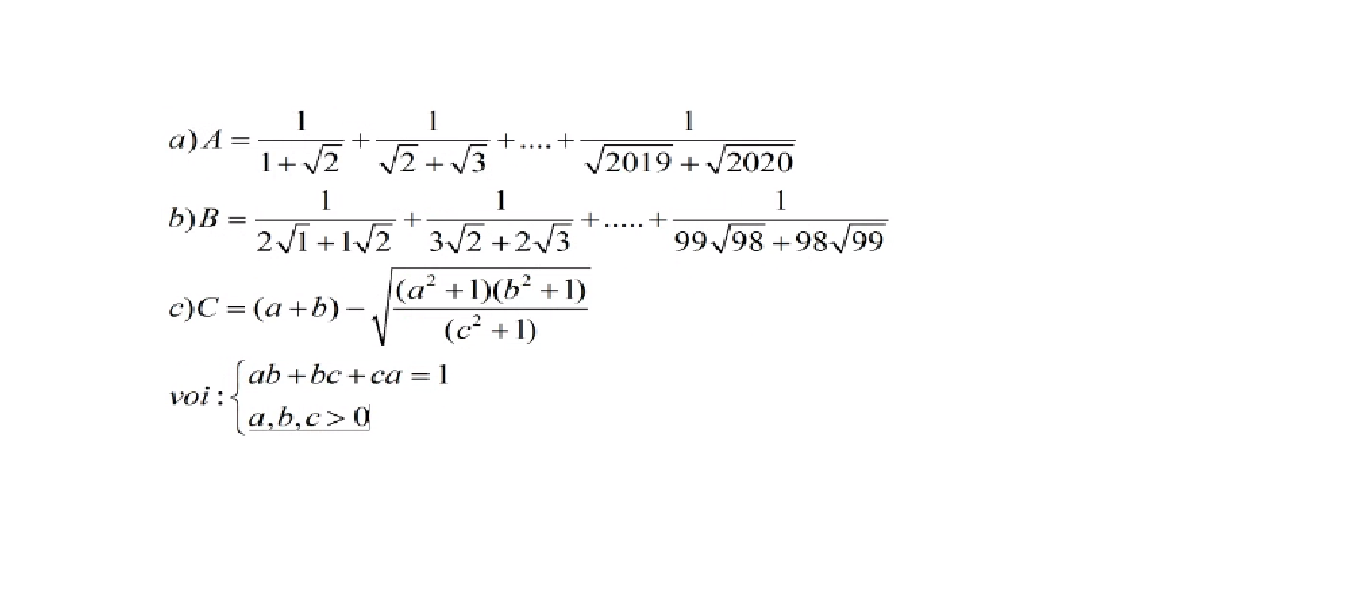b Ta có \(\dfrac{1}{\left(n+1\right)\sqrt{n}+n\sqrt{n+1}}=\dfrac{\left(n+1\right)\sqrt{n}-n\sqrt{n+1}}{\left(n+1\right)^2n-n^2\left(n+1\right)}=\dfrac{\left(n+1\right)\sqrt{n}-n\sqrt{n+1}}{n^3+2n^2+n-n^3-n^2}=\dfrac{\left(n+1\right)\sqrt{n}-n\sqrt{n+1}}{n\left(n+1\right)}=\dfrac{1}{\sqrt{n}}-\dfrac{1}{\sqrt{n+1}}\forall n>0\) Áp dụng công thức trên ta được: \(\dfrac{1}{2\sqrt{1}+1\sqrt{2}}=\dfrac{1}{\sqrt{1}}-\dfrac{1}{\sqrt{2}}=1-\dfrac{1}{\sqrt{2}}\)
\(\dfrac{1}{3\sqrt{2}+2\sqrt{3}}=\dfrac{1}{\sqrt{2}}-\dfrac{1}{\sqrt{3}}\) .... \(\dfrac{1}{99\sqrt{98}+98\sqrt{99}}=\dfrac{1}{\sqrt{98}}-\dfrac{1}{\sqrt{99}}\) \(\Rightarrow B=1-\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{2}}-\dfrac{1}{\sqrt{3}}+...+\dfrac{1}{\sqrt{98}}-\dfrac{1}{\sqrt{99}}=1-\dfrac{1}{3\sqrt{11}}=\dfrac{3\sqrt{11}-1}{3\sqrt{11}}=\dfrac{33-\sqrt{11}}{33}\)c . \(\Rightarrow C=\left(a+b\right)-\sqrt{\dfrac{\left(a^2+ab+bc+ca\right)\left(b^2+ab+bc+ca\right)}{c^2+ab+bc+ca}}=a+b-\sqrt{\dfrac{\left(a+b\right)\left(a+c\right)\left(b+c\right)\left(b+a\right)}{\left(c+b\right)\left(c+a\right)}}=a+b-\sqrt{\left(a+b\right)^2}=a+b-a-b=0\)