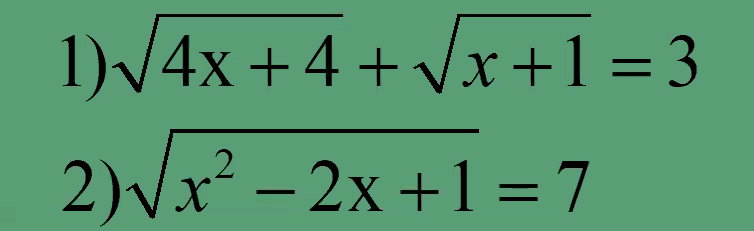a, ĐK : x >= -1
\(\Leftrightarrow2\sqrt{x+1}+\sqrt{x+1}=3\Leftrightarrow3\sqrt{x+1}=3\)
\(\Leftrightarrow\sqrt{x+1}=1\Leftrightarrow x+1=1\Leftrightarrow x=0\)
b, \(\sqrt{x^2-2x+1}=7\Leftrightarrow\left|x-1\right|=7\)
TH1 : \(x-1=7\Leftrightarrow x=8\)
TH2 : \(x-1=-7\Leftrightarrow x=-6\)
1,\(\sqrt{4x+4}+\sqrt{x+1}=3\)
\(\Leftrightarrow\sqrt{4\left(x+1\right)}+\sqrt{x+1}=3\)
\(\Leftrightarrow2\sqrt{x+1}+\sqrt{x+1}=3\)
\(\Leftrightarrow\left(\sqrt{x+1}\right)\left(2+1\right)=3\)
\(\Leftrightarrow3\sqrt{x+1}=3\)
\(\Leftrightarrow\sqrt{x+1}=1\) ĐK:\(x+1\ge0\Rightarrow x\ge-1\)
\(\Leftrightarrow\left(\sqrt{x+1}\right)^2=1^2\)
\(\Leftrightarrow x+1=1\)
\(\Leftrightarrow x=0\)(TMĐK)
Vậy tập nghiệm của phương trình là S={0}
b,\(\sqrt{x^2-2x+1}=7\)
\(\Leftrightarrow\sqrt{\left(x-1\right)^2}=7\)
\(\Leftrightarrow\left|x-1\right|=7\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=7\\x-1=-7\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=8\\x=-6\end{matrix}\right.\)
Vậy tập nghiệm của phương trình là S={8;-6}
1) Ta có: \(\sqrt{4x+4}+\sqrt{x+1}=3\)
\(\Leftrightarrow3\sqrt{x+1}=3\)
\(\Leftrightarrow x+1=1\)
hay x=0
2) Ta có: \(\sqrt{x^2-2x+1}=7\)
\(\Leftrightarrow\left|x-1\right|=7\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=7\\x-1=-7\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=8\\x=-6\end{matrix}\right.\)