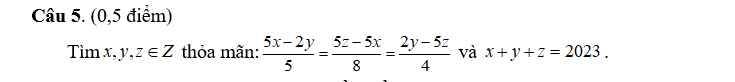Bài 8: Tính chất của dãy tỉ số bằng nhau

Gọi số bi của Minh, Dũng, Hùng lần lượt là a,b,c

Theo đề, ta có: a/2=b/4=c/5 và 3b-2a=40

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{a}{2}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{3b-2a}{3\cdot4-2\cdot2}=\dfrac{40}{12-4}=5\)

=>a=10; b=20; c=25

Gọi số viên bi của ba bạn Minh, Dũng, Hùng lần lượt là a, b, c (viên bi; a, b, c ∈ N*)

Vì số viên bi của 3 bạn Minh, Dũng, Hùng tỉ lệ với các số 2, 4, 5 và 3 lần số bi của bạn Dũng nhiều hơn hai lần số bi của bạn Minh là 40 viên bi nên:

\(\dfrac{a}{2}=\dfrac{b}{4}=\dfrac{c}{5}\) và 3b - 2a = 40

Áp dụng tính chât của dãy tỉ số bằng nhau và 3b - 2a = 40, ta được:

\(\dfrac{a}{2}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{3b}{12}=\dfrac{2a}{4}=\dfrac{3b-2a}{12-4}=\dfrac{40}{8}=5\)

\(\Rightarrow\left\{{}\begin{matrix}\dfrac{a}{2}=5\\\dfrac{b}{4}=5\\\dfrac{c}{5}=5\end{matrix}\right.\)                                \(\Rightarrow\left\{{}\begin{matrix}a=10\\b=20\\c=25\end{matrix}\right.\)(thoả mãn điều kiện a, b, c ∈ N*)

Vậy...

các bạn giải thích dùm mình nhé.. chưa hiểu lắm. tks

Ta có: 

\(3x=5y\Rightarrow\dfrac{x}{5}=\dfrac{y}{3}\)

\(6y=4z\Rightarrow3y=2z\Rightarrow\dfrac{y}{2}=\dfrac{z}{3}\)

Mà: \(\dfrac{x}{10}=\dfrac{y}{6};\dfrac{y}{6}=\dfrac{z}{9}\)

\(\Rightarrow\dfrac{x}{10}=\dfrac{y}{6}=\dfrac{z}{9}\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

\(\dfrac{x+y-z}{10+6-9}=\dfrac{2}{7}\)

\(\Rightarrow\dfrac{x}{10}=\dfrac{2}{7}\Rightarrow x=\dfrac{20}{7}\)

\(\Rightarrow\dfrac{y}{6}=\dfrac{2}{7}\Rightarrow y=\dfrac{12}{7}\)

\(\Rightarrow\dfrac{z}{9}=\dfrac{2}{7}\Rightarrow z=\dfrac{18}{7}\)

Sửa đề: \(\dfrac{y}{5}=\dfrac{z}{4};x-y+z=-49\)

\(\dfrac{x}{2}=\dfrac{y}{3}\) nên \(\dfrac{x}{10}=\dfrac{y}{15}\)

\(\dfrac{y}{5}=\dfrac{z}{4}\) nên \(\dfrac{y}{15}=\dfrac{z}{12}\)

=>\(\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{12}\)

mà x-y+z=-49

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{12}=\dfrac{x-y+z}{10-15+12}=-\dfrac{49}{7}=-7\)

=>\(x=-7\cdot10=-70;y=-7\cdot15=-105;z=-7\cdot12=-84\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

\(\dfrac{x}{3}=\dfrac{y}{6}=\dfrac{z}{15}=\dfrac{2x-3y+z}{2\cdot3-3\cdot6+15}=\dfrac{2}{3}\)

\(\Rightarrow\dfrac{x}{3}=\dfrac{2}{3}\Rightarrow x=2\)

\(\Rightarrow\dfrac{y}{6}=\dfrac{2}{3}\Rightarrow y=4\)

\(\Rightarrow\dfrac{z}{15}=\dfrac{2}{3}\Rightarrow z=10\)

Ta có : 

`x/3 =y/6 =z/15=> (2x)/6= (3y)/18 = z/15`

Vậy `(2x)/6= (3y)/18 = z/15` và `2x-3y+z=2`

ADTC dãy tỉ số bằng nhau ta có :

`(2x)/6= (3y)/18 = z/15 =(2x-3y+z)/(6-18+15)=2/3`

`=> x/3=2/3=> x= 2/3 . 3= 2`

`=> y/6=2/3=>y=2/3 . 6= 4`

`=> z/15=2/3=> z=2/3 . 15=10`

Lời giải:
a. Đặt $\frac{x}{3}=\frac{y}{7}=k\Rightarrow x=3k; y=7k$. Khi đó:

$x^2+y^2=58$

$\Rightarrow (3k)^2+(7k)^2=58$

$\Rightarrow 58k^2=58$

$\Rightarrow k^2=1\Rightarrow k=\pm 1$

Nếu $k=1$ thì $x=3k=3; y=7k=7$

Nếu $k=-1$ thì $x=3k=-3; y=7k=-7$

b.

Đặt $\frac{x}{3}=\frac{y}{4}=k\Rightarrow x=3k; y=4k$

Khi đó:

$x^3-y^3=37$

$\Rightarrow (3k)^3-(4k)^3=37$

$\Rightarrow -37k^3=37\Rightarrow k^3=-1\Rightarrow k=-1$

Khi đó:

$x=3k=-3; y=4k=-4$

a,Áp dụng tính chất dãy tỉ số bằng nhau ta có:

\(\dfrac{x}{3}=\dfrac{y}{7}=\dfrac{x^2+y^2}{3^2+7^2}=\dfrac{58}{58}=1\\ \Rightarrow\left\{{}\begin{matrix}\dfrac{x}{3}=1\Rightarrow x=3\\\dfrac{y}{7}=1\Rightarrow y=7\end{matrix}\right.\)

Vậy x=3;y=7

b,Áp dụng tính chất dãy tỉ số bằng nhau ta có:

\(\dfrac{x}{3}=\dfrac{y}{7}=\dfrac{x^3-y^3}{3^3-4^3}=\dfrac{37}{-37}=-1\\ \Rightarrow\left\{{}\begin{matrix}\dfrac{x}{3}=-1\Rightarrow x=-3\\\dfrac{y}{4}=-1\Rightarrow y=-4\end{matrix}\right.\)

Vậy x=-3;y=-4

Cách kết bạn

Bạn xem lại đề bài, \(x+y+z=2025?\) không phải là \(x+y+z=2023\). Thanks!

Bài 1:

\(2\cdot162=6\cdot54\)

=>Lập được 4 tỉ lệ thức

\(2\cdot54=6\cdot18\)

=>Lập được 4 tỉ lệ thức

\(6\cdot162=18\cdot54\)

=>Lập được 4 tỉ lệ thức

=>Tổng cộng lập được 4+4+4=12 tỉ lệ thức

Bài 2:

a: ĐKXĐ: x<>-4

\(\dfrac{x-6}{x+4}=\dfrac{2}{7}\)

=>\(7\left(x-6\right)=2\left(x+4\right)\)

=>\(7x-42=2x+8\)

=>5x=50

=>x=10(nhận)

b: ĐKXĐ: x<>-5

\(\dfrac{x+5}{2\dfrac{1}{2}}=\dfrac{40}{x+5}\)

=>\(\left(x+5\right)^2=40\cdot\dfrac{5}{2}=100\)

=>\(\left[{}\begin{matrix}x+5=10\\x+5=-10\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\left(nhận\right)\\x=-15\left(nhận\right)\end{matrix}\right.\)

c: ĐKXĐ: x<>0

\(\dfrac{15}{x^6}:\dfrac{1}{8}=2.5:\dfrac{2}{3}x\)

=>\(\dfrac{120}{x^6}=2,5:\dfrac{2x}{3}=\dfrac{5}{2}\cdot\dfrac{3}{2x}=\dfrac{15}{4x}\)

=>\(\dfrac{8}{x^5}=\dfrac{1}{4}\)

=>\(x^5=8\cdot\dfrac{4}{1}=32\)

=>x=2(nhận)

d: \(\left\{{}\begin{matrix}x:y=4,5:\left(-3\right)\\y:z=-\dfrac{1}{3}:\dfrac{1}{4}\\z:\dfrac{6}{5}=\dfrac{5}{8}:\dfrac{1}{4}\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}\dfrac{x}{y}=\dfrac{4.5}{-3}=-\dfrac{3}{2}\\\dfrac{y}{z}=-\dfrac{1}{3}\cdot4=-\dfrac{4}{3}\\z=5\cdot\dfrac{4}{8}\cdot\dfrac{6}{5}=6\cdot\dfrac{1}{2}=3\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}z=3\\y=-\dfrac{4}{3}\cdot z=-\dfrac{4}{3}\cdot3=-4\\x=-\dfrac{3}{2}\cdot y=-\dfrac{3}{2}\cdot\left(-4\right)=6\end{matrix}\right.\)