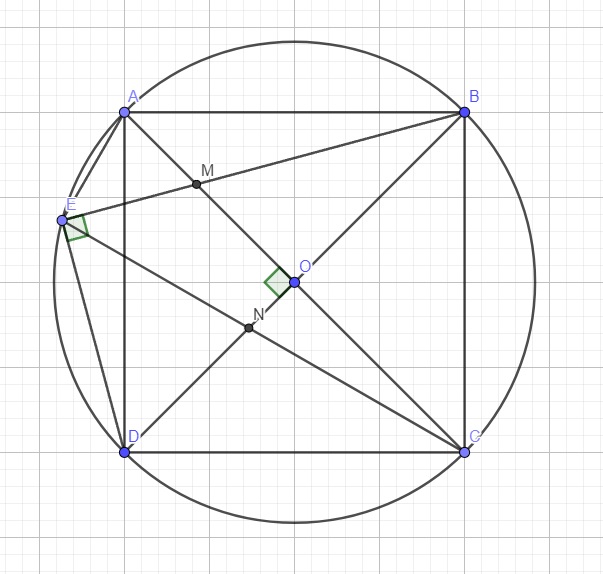
a.
ABCD là hình vuông nội tiếp đường tròn (O) \(\Rightarrow AC;BD\) là các đường kính
\(\Rightarrow\widehat{BEM}\) là góc nt chắn nửa đường tròn
\(\Rightarrow\widehat{BEM}=90^0\) hay \(\widehat{MED}=90^0\)
Cũng do ABCD là hình vuông \(\Rightarrow AC\perp BD\) tại O \(\Rightarrow\widehat{MOD}=90^0\)
\(\Rightarrow O,E\) cùng nhìn MD dưới 1 góc vuông
\(\Rightarrow OMED\) nội tiếp.
b.
Do OMED nội tiếp \(\Rightarrow\widehat{EMO}+\widehat{EDO}=180^0\)
Mà \(\widehat{BMC}+\widehat{EMO}=180^0\) (kề bù)
\(\Rightarrow\widehat{BMC}=\widehat{EDO}\)
Lại có \(\widehat{EDO}=\widehat{BCN}\) (cùng chắn cung BE của (O))
\(\Rightarrow\widehat{BMC}=\widehat{BCN}\) (1)
Tứ giác ABCE nội tiếp (O) \(\Rightarrow\widehat{BAE}+\widehat{BCN}=180^0\) (2)
\(\widehat{BMA}+\widehat{BMC}=180^0\) (kề bù) (3)
(1);(2);(3) \(\Rightarrow\widehat{BMA}=\widehat{BAE}\)
Xét hai tam giác AMB và EAB có:
\(\left\{{}\begin{matrix}\widehat{ABM}-chung\\\widehat{BMA}=\widehat{BAE}\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta AMB\sim\Delta EAB\left(g.g\right)\)