Question

Cho hbh ABCD có E,F lần lượt làtrung điểm của  AB , CD 

CMR

a)AF//EC 

b)ED=BF

c)AC cát ED tại O . CM E.O.F thẳng hàng

d)AF cắt ED tại O , BF cắt EC tại H . CMR G,O,H thẳng hàn

Answer 1

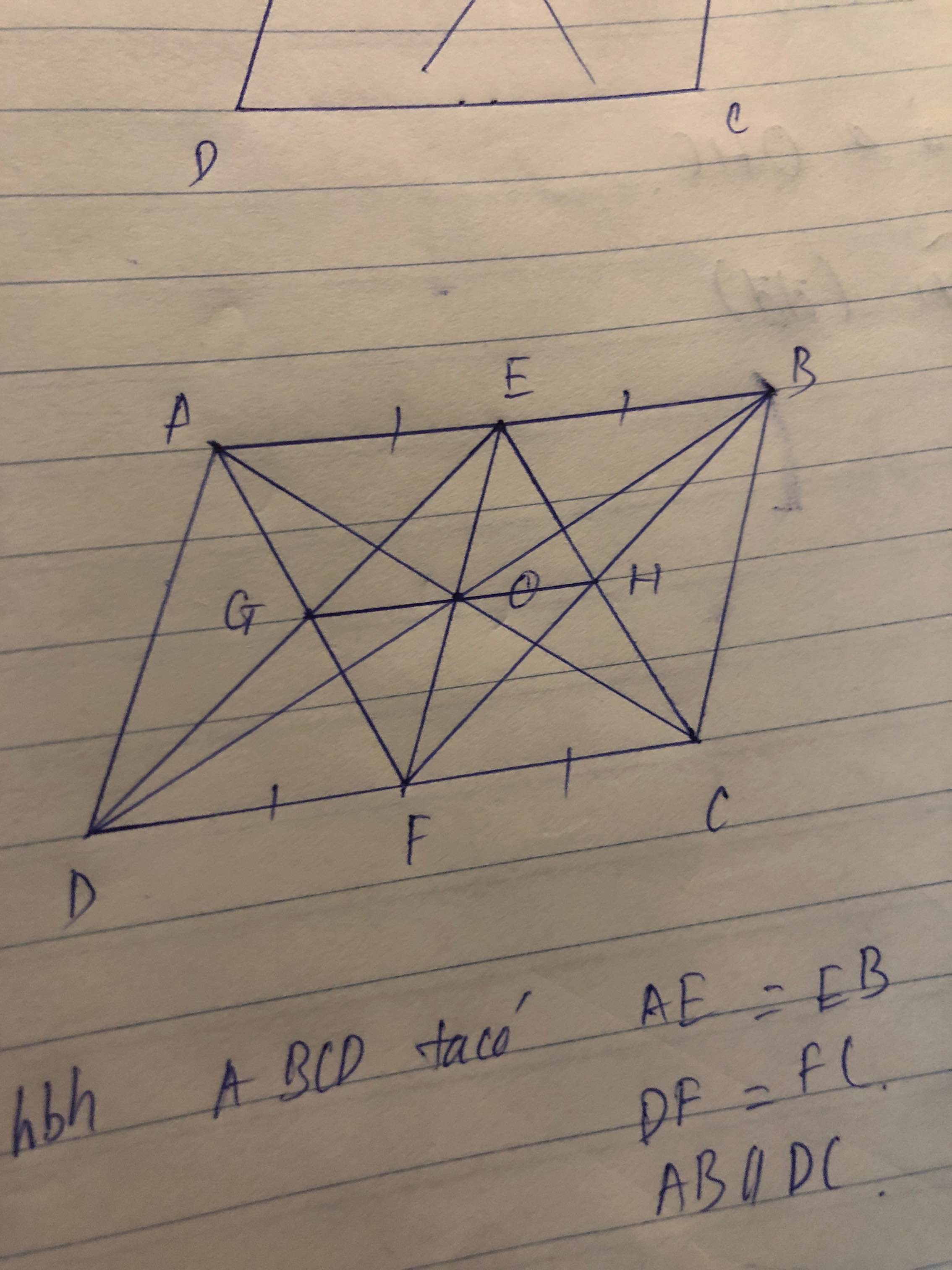
Sao AC cắt ED tại O mà AF cx cắt ED tại O z?

Answer 2

Answer 3

Lần sau e ktra lại đề kĩ trước ghi đăng lên nhé

a) Xét tứ giác AECF có:

AE//CF(ABCD là hbh)

AE=CF\(=\dfrac{1}{2}AB=\dfrac{1}{2}DC\)

=> AECF là hbh

=> AF//EC

b) Xét tứ giác EBFD có:

EB//DF(ABCD là hình bình hành)

EB=DF\(=\dfrac{1}{2}AB=\dfrac{1}{2}DC\)

=> EBFD là hbh

=> ED=BF

c) Sửa: AD cắt DB tại O

O là giao điểm 2 đường chéo hbh

=> O là trung điểm BD

=> OF là đường trung bình của tam giác DBC

Và OE là đường trung bình tam giác AOB

=> OF//AD//BC, OE//AD//BC

=> O,E,F thẳng hàng(tiên đề Ơ-clit)

d) Xét tứ giác AEFD có:

AE//DF

AE=DF \(=\dfrac{1}{2}AB=\dfrac{1}{2}DC\)

=> AEFD là hbh

=> G là trung điểm ED

CMTT: EBCF là hbh

=> H là trung điểm EC

Xét tam giác ADF có:

O là trung điểm EF

G là trung điểm EO

=> OG là đường trung bình

=> OG//DC

CMTT: OH là đường trung bình

=> OH//DC

=> G,O,H thẳng hàng(tiên đề Ơ-clit)