Question

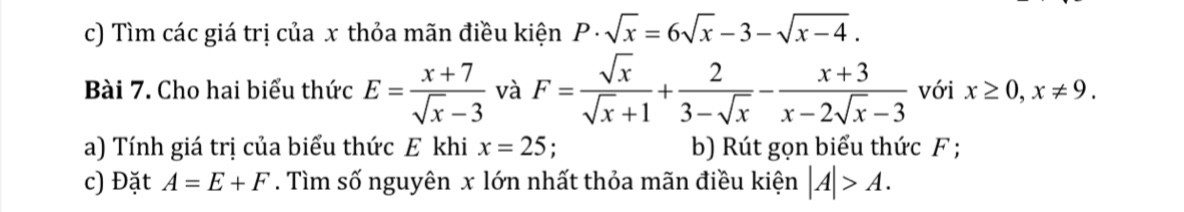
c) Tìm các giá trị của \( x \) thỏa mãn điều kiện \( P \cdot \sqrt{x} = 6 \sqrt{x} - 3 - \sqrt{x - 4} \).

Bài 7. Cho hai biểu thức \( E = \frac{x+7}{\sqrt{x-3}} \) và \( F = \frac{\sqrt{x}}{\sqrt{x+1}} + \frac{2}{3-\sqrt{x}} - \frac{x+3}{x-2\sqrt{x-3}} \) với \( x \geq 0, x \neq 9 \).

a) Tính giá trị của biểu thức \( E \) khi \( x = 25 \);

b) Rút gọn biểu thức \( F \);

c) Đặt \( A = E + F \). Tìm số nguyên \( x \) lớn nhất thỏa mãn điều kiện \( |A| > A \).

Answer 1

a. thay x = 25 vào E ta được:

\(E=\dfrac{x+7}{\sqrt{x}-3}=\dfrac{25+7}{\sqrt{25}-3}=\dfrac{32}{2}=16\)

b. \(F=\dfrac{\sqrt{x}}{\sqrt{x}+1}+\dfrac{2}{3-\sqrt{x}}-\dfrac{x+3}{x-2\sqrt{x}-3}\)

\(=\dfrac{\sqrt{x}}{\sqrt{x}+1}-\dfrac{2}{\sqrt{x}-3}-\dfrac{x+3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+1\right)}\\ =\dfrac{\sqrt{x}\cdot\left(\sqrt{x}-3\right)-2\cdot\left(\sqrt{x}+1\right)-x-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+1\right)}\\ =\dfrac{x-3\sqrt{x}-2\sqrt{x}-2-x-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+1\right)}\\ =\dfrac{-5\sqrt{x}-5}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+1\right)}\\ =\dfrac{-5\cdot\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+1\right)}\\ =\dfrac{-5}{\sqrt{x}-3}\)

c. \(A=E+F=\dfrac{x+7}{\sqrt{x}-3}+\dfrac{-5}{\sqrt{x}-3}=\dfrac{x+2}{\sqrt{x}-3}\)

để \(\left|A\right|>A\text{ thì }A< 0\)

x + 2 > 2 ≥ 0 => x ≥ 0 (1)

\(\sqrt{x}-3< 0\Rightarrow\sqrt{x}< 3\Rightarrow x< 9\) (2)

từ (1) (2) => x ∈ {0; 1; 2; 3; 4; 5; 6; 7; 8}

vậy số nguyên x lớn nhất cần tìm là 8