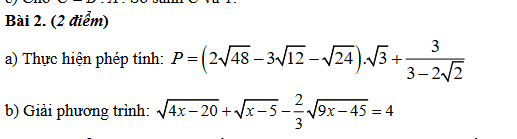a: \(P=\left(2\sqrt{48}-3\sqrt{12}-\sqrt{24}\right)\cdot\sqrt{3}+\dfrac{3}{3-2\sqrt{2}}\)
\(=\left(2\cdot4\sqrt{3}-3\cdot2\sqrt{3}-2\sqrt{6}\right)\cdot\sqrt{3}+3\left(3+2\sqrt{2}\right)\)
\(=\left(8\sqrt{3}-6\sqrt{3}-2\sqrt{6}\right)\cdot\sqrt{3}+3\left(3+2\sqrt{2}\right)\)
\(=\left(2\sqrt{3}-2\sqrt{6}\right)\cdot\sqrt{3}+9+6\sqrt{2}\)
\(=6-2\sqrt{18}+9+6\sqrt{2}=15\)
b: ĐKXĐ: x>=5
\(\sqrt{4x-20}+\sqrt{x-5}-\dfrac{2}{3}\cdot\sqrt{9x-45}=4\)
=>\(2\sqrt{x-5}+\sqrt{x-5}-\dfrac{2}{3}\cdot3\sqrt{x-5}=4\)
=>\(\sqrt{x-5}=4\)
=>x-5=16
=>x=16+5=21(nhận)
Đúng 2
Bình luận (1)
