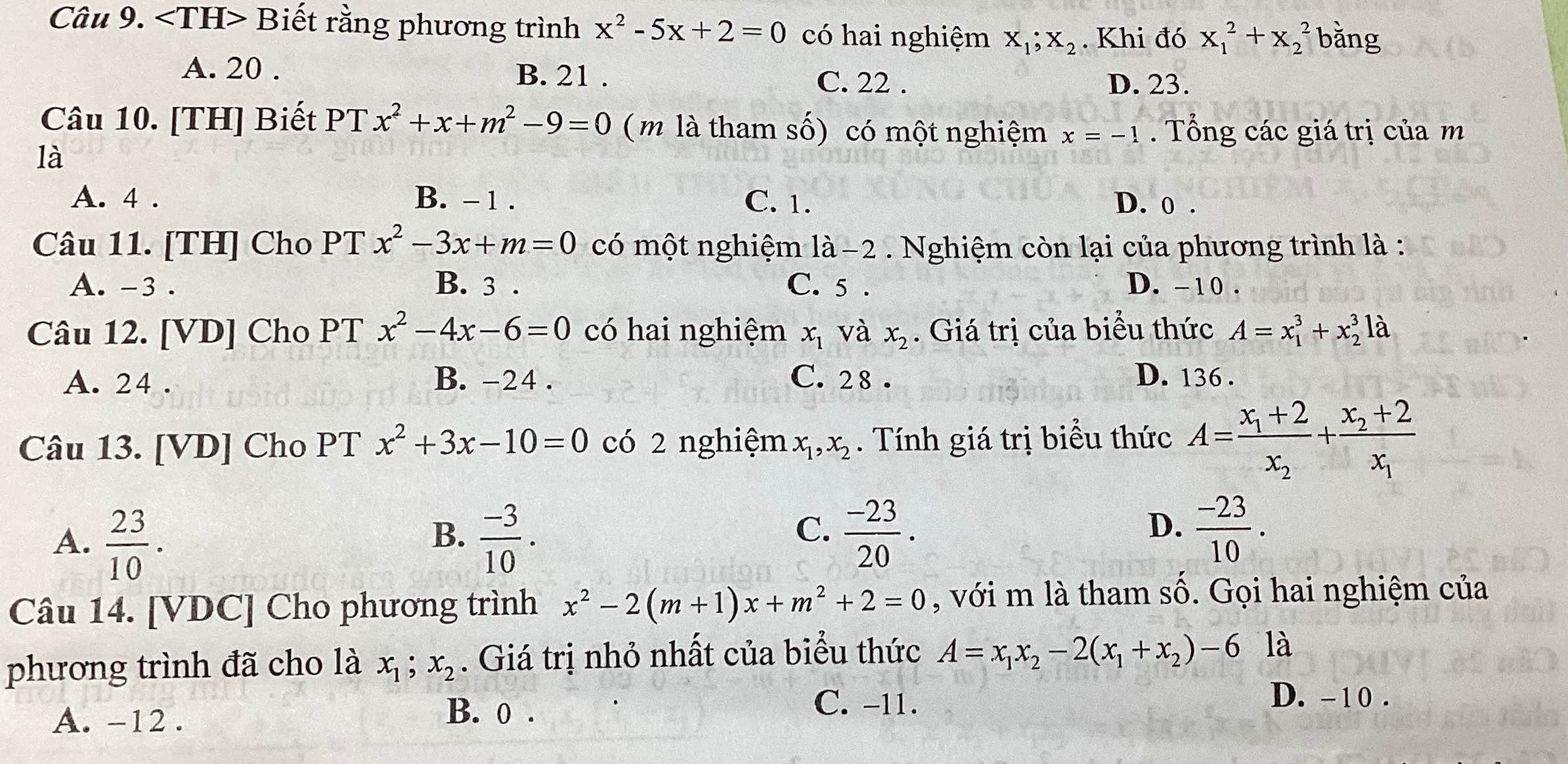Câu 9: \(x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=5^2-2\cdot2=25-4=21\)
=>Chọn B
Câu 10: Thay x=-1 vào phương trình, ta được:
\(\left(-1\right)^2+\left(-1\right)+m^2-9=0\)
=>\(m^2-9=0\)
=>\(\left[{}\begin{matrix}m=3\\m=-3\end{matrix}\right.\)
Tổng các giá trị của m là (-3)+3=0
=>Chọn D
Câu 11:
Thay x=-2 vào phương trình, ta được:
\(\left(-2\right)^2-3\cdot\left(-2\right)+m=0\)
=>m+4+6=0
=>m=-10
=>Phương trình sẽ là \(x^2-3x-10=0\)
=>(x-5)(x+2)=0
=>x=5 hoặc x=-2
=>Nghiệm còn lại là x=5
=>Chọn C
Câu 12: Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=4\\x_1x_2=\dfrac{c}{a}=-6\end{matrix}\right.\)
\(A=x_1^3+x_2^3\)
\(=\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)\)
\(=4^3-3\cdot4\cdot\left(-6\right)=64+12\cdot6=64+72=136\)
=>Chọn D
Câu 13:
Theo Vi-et, ta có: \(x_1+x_2=-\dfrac{b}{a}=-3;x_1x_2=\dfrac{c}{a}=-10\)
\(A=\dfrac{x_1+2}{x_2}+\dfrac{x_2+2}{x_1}\)
\(=\dfrac{x_1^2+2x_1+x_2^2+2x_2}{x_1x_2}\)
\(=\dfrac{\left(x_1+x_2\right)^2-2x_1x_2+2\left(x_1+x_2\right)}{x_1x_2}\)
\(=\dfrac{\left(-3\right)^2-2\cdot\left(-10\right)+2\cdot\left(-3\right)}{-10}=\dfrac{9+20-6}{-10}=\dfrac{23}{-10}=-\dfrac{23}{10}\)
=>Chọn D
Câu 14:
\(\Delta=\left[-2\left(m+1\right)\right]^2-4\left(m^2+2\right)\)
\(=4\left(m^2+2m+1\right)-4\left(m^2+2\right)\)
\(=4m^2+8m+4-4m^2-8=8m-4\)
Để phương trình có hai nghiệm phân biệt thì 8m-4>0
=>8m>4
=>\(m>\dfrac{1}{2}\)
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2\left(m+1\right)=2m+2\\x_1x_2=\dfrac{c}{a}=m^2+2\end{matrix}\right.\)
\(A=x_1x_2-2\left(x_1+x_2\right)-6\)
\(=m^2+2-2\left(2m+2\right)-6=m^2-4-4m-4\)
\(=m^2-4m+4-12=\left(m-2\right)^2-12>=-12\forall m\)
Dấu '=' xảy ra khi m=2
=>Chọn A