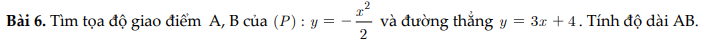Phương trình hoành độ giao điểm là:
\(-\dfrac{x^2}{2}=3x+4\)
=>\(\dfrac{x^2}{2}+3x+4=0\)
=>\(x^2+6x+8=0\)
=>(x+2)(x+4)=0
=>\(\left[{}\begin{matrix}x=-2\\x=-4\end{matrix}\right.\)
Khi x=-2 thì \(y=3\cdot\left(-2\right)+4=-6+4=-2\)
Khi x=-4 thì \(y=3\cdot\left(-4\right)+4=-12+4=-8\)
vậy: A(-2;-2); B(-4;-8)
\(AB=\sqrt{\left(-4+2\right)^2+\left(-8+2\right)^2}=\sqrt{\left(-2\right)^2+\left(-6\right)^2}=2\sqrt{10}\)
Đúng 1
Bình luận (0)
