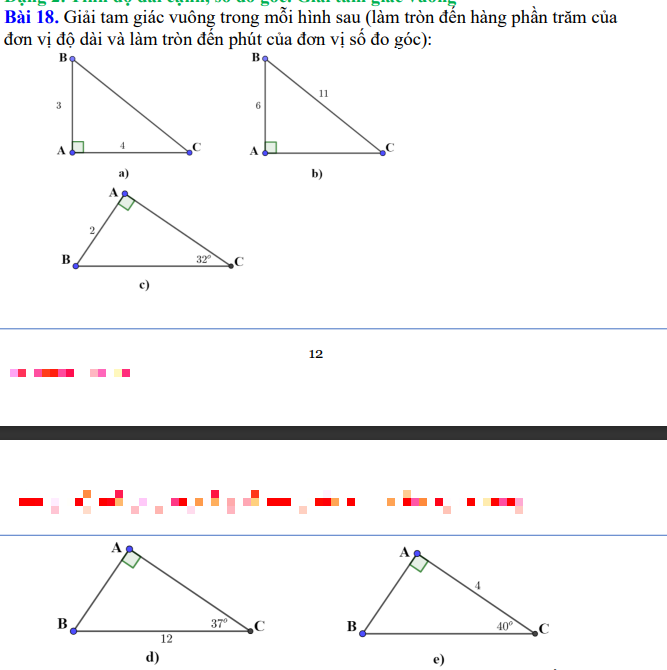
a: ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
=>\(BC=\sqrt{3^2+4^2}=5\)
Xét ΔABC vuông tại A có \(sinC=\dfrac{AB}{BC}=\dfrac{3}{5}\)
nên \(\widehat{C}\simeq36^052'\)
ΔABC vuông tại A
=>\(\widehat{B}+\widehat{C}=90^0\)
=>\(\widehat{B}\simeq90^0-36^052'=53^08'\)
b:
Xét ΔABC vuông tại A có \(sinC=\dfrac{AB}{BC}=\dfrac{6}{11}\)
nên \(\widehat{C}\simeq33^03'\)
ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ABC}=90^0-33^03'=56^057'\)
ΔABC vuông tại A
=>\(AC^2+AB^2=BC^2\)
=>\(AC=\sqrt{11^2-6^2}\simeq9,22\)
c:
ΔABC vuông tại A
=>\(\widehat{B}+\widehat{C}=90^0\)
=>\(\widehat{B}=90^0-32^0=58^0\)
Xét ΔABC vuông tại A có \(tanC=\dfrac{AB}{AC}\)
=>\(AC=\dfrac{2}{tan32}\simeq3,20\)
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC=\sqrt{AB^2+AC^2}\simeq3,77\)
d:
ΔABC vuông tại A
=>\(\widehat{B}+\widehat{C}=90^0\)
=>\(\widehat{B}=90^0-37^0=53^0\)
Xét ΔABC vuông tại A có \(sinC=\dfrac{AB}{BC}\)
=>\(AB=12\cdot sin37\simeq7,22\)
Xét ΔABC vuông tại A có \(cosC=\dfrac{AC}{BC}\)
=>\(AC=12\cdot cos37\simeq9,58\)
e:
ΔABC vuông tại A
=>\(\widehat{B}+\widehat{C}=90^0\)
=>\(\widehat{B}=90^0-40^0=50^0\)
Xét ΔABC vuông tại A có \(tanC=\dfrac{AB}{AC}\)
=>\(AB=AC\cdot tanC=4\cdot tan40\simeq3,36\)
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC=\sqrt{AB^2+AC^2}\simeq5,22\)