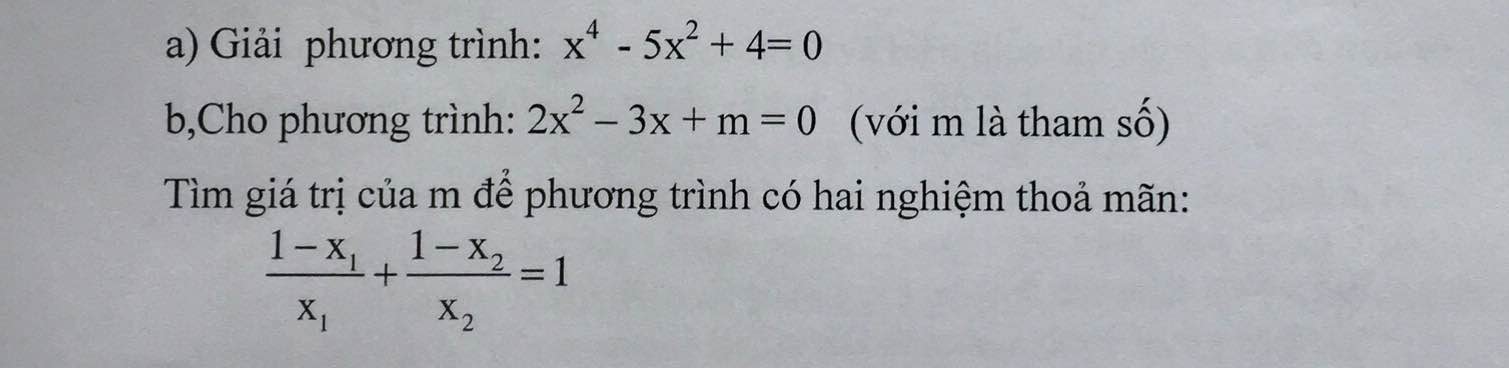Question

Answer 1

a) Đặt t = x² (t ≥ 0).

Khi đó pt tương đương với t² - 5t + 4 = 0

Giải pt ta được t = 1; t = 4. Suy ra x ∈ {-2; -1; 1; 2}.

b) Để phương trình có hai nghiệm thì △ = (-3)² - 4.2.m ≥ 0 hay 9 - 8m ≥ 0.

hay m ≤ \(\dfrac{9}{8}\).

Theo hệ thức Viet ta có: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{3}{2}\\x_1\cdot x_2=\dfrac{m}{2}\end{matrix}\right.\)

\(\dfrac{1-x_1}{x_1}+\dfrac{1-x_2}{x_2}=1\Leftrightarrow\dfrac{1}{x_1}+\dfrac{1}{x_2}-2=1hay\dfrac{1}{x_1}+\dfrac{1}{x_2}=3\)

\(\dfrac{1}{x_1}+\dfrac{1}{x_2}=\dfrac{x_1+x_2}{x_1\cdot x_2}=\dfrac{3}{m}=3\) Suy ra m = 1 (tmdk).