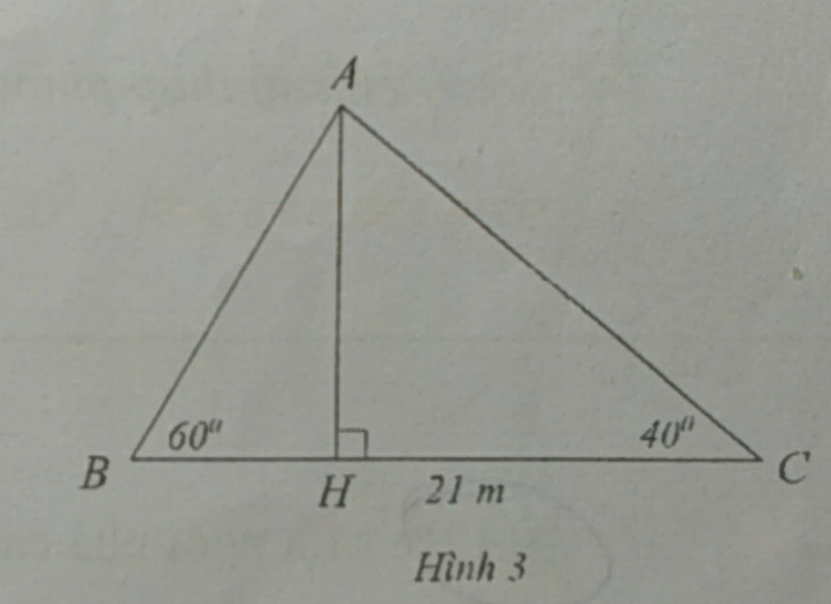
Bài 26:
a: Xét ΔAHB vuông tại H có \(tanB=\dfrac{AH}{HB}\)
=>\(HB=\dfrac{AH}{tanB}=\dfrac{AH}{tan60}\)
Xét ΔAHC vuông tại H có \(tanC=\dfrac{AH}{HC}\)
=>\(HC=\dfrac{AH}{tanC}=\dfrac{AH}{tan40}\)
HB+HC=BC
=>\(AH\left(\dfrac{1}{tan60}+\dfrac{1}{tan40}\right)=21\)
=>\(AH=21:\left(\dfrac{1}{tan60}+\dfrac{1}{tan40}\right)\simeq11,87\left(cm\right)\)
Xét ΔAHC vuông tại H có \(sinC=\dfrac{AH}{AC}\)
=>\(AC=\dfrac{AH}{sinC}\simeq18,47\left(cm\right)\)
b: Diện tích tam giác ABC là:
\(S_{BAC}=\dfrac{1}{2}\cdot CA\cdot CB\cdot sinC=\dfrac{1}{2}\cdot18,47\cdot21\cdot sin40\simeq124,66\left(cm^2\right)\)