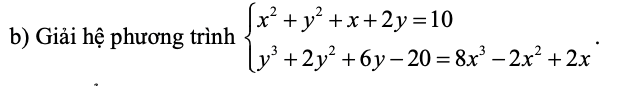\(\Leftrightarrow\left\{{}\begin{matrix}2x^2+2y^2=20-2x-4y\\y^3+2x^2+2y^2+6y-20=8x^3+2x\end{matrix}\right.\)
\(\Rightarrow y^3+\left(20-2x-4y\right)+6y-20=8x^3+2x\)
\(\Leftrightarrow y^3+2y=8x^3+4x\)
\(\Leftrightarrow8x^3-y^3+4x-2y=0\)
\(\Leftrightarrow\left(2x-y\right)\left(4x^2+2xy+y^2\right)+2\left(2x-y\right)=0\)
\(\Leftrightarrow\left(2x-y\right)\left(4x^2+2xy+y^2+2\right)=0\)
\(\Leftrightarrow\left(2x-y\right)\left(3x^2+\left(x+y\right)^2+2\right)=0\)
\(\Leftrightarrow2x-y=0\)
\(\Rightarrow y=2x\)
Thay vào pt đầu:
\(x^2+\left(2x\right)^2+x+2.\left(2x\right)=10\)
\(\Leftrightarrow5x^2+5x-10=0\Rightarrow\left[{}\begin{matrix}x=1\Rightarrow y=2\\x=-2\Rightarrow y=-4\end{matrix}\right.\)