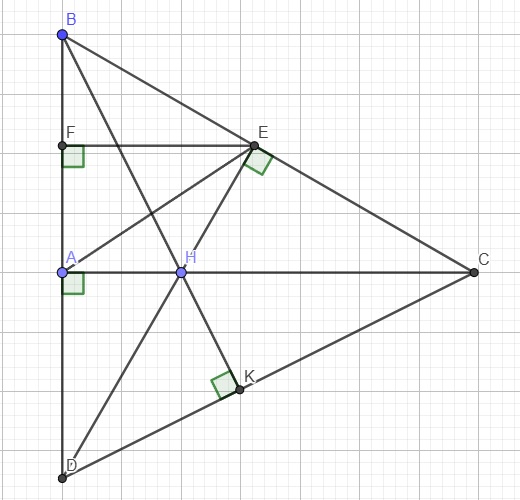
a.
Trong tam giác vuông ABC:
\(cosB=\dfrac{AB}{BC}=\dfrac{1}{2}\Rightarrow B=60^0\)
Áp dụng định lý Pitago:
\(AC=\sqrt{BC^2-AB^2}=2\sqrt{3}\left(cm\right)\)
b.
Do \(\left\{{}\begin{matrix}CA\perp AB\left(gt\right)\\BK\perp CK\left(gt\right)\end{matrix}\right.\)
Mà H là giao điểm CA và BK
\(\Rightarrow H\) là trực tâm tam giác BCD
\(\Rightarrow DH\) là đường cao thứ 3 của tam giác BCD
\(\Rightarrow DH\perp BC\) tại E
\(\Rightarrow\widehat{BCK}=\widehat{DHK}\) (cùng phụ \(\widehat{HDK}\)) (1)
Xét hai tam giác DKH và BKC có:
\(\left\{{}\begin{matrix}\widehat{DHK}=\widehat{BCK}\left(cmt\right)\\\widehat{DKH}=\widehat{BKC}=90^0\end{matrix}\right.\)
\(\Rightarrow\Delta DKH=\Delta BKC\left(g.g\right)\)
Trong tam giác vuông DKH:
\(sin\widehat{DHK}=\dfrac{DK}{DH}\Rightarrow DK=DH.sin\widehat{DHK}\) (2)
(1);(2) \(\Rightarrow DK=DH.sin\widehat{BCK}\)
c.
Từ E kẻ \(EF\perp AB\)
Trong tam giác vuông BDE:
\(cosB=\dfrac{BE}{BD}\Rightarrow BE=BD.cosB=3.cos60^0=\dfrac{3}{2}\left(cm\right)\)
Trong tam giác vuông BEF:
\(sinB=\dfrac{EF}{BE}\Rightarrow EF=BE.sinB=\dfrac{3}{2}.sin60^0=\dfrac{3\sqrt{3}}{4}\left(cm\right)\)
Do đó:
\(S_{\Delta ABE}=\dfrac{1}{2}EF.AB=\dfrac{1}{2}.\dfrac{3\sqrt{3}}{4}.2=\dfrac{3\sqrt{3}}{4}\left(cm^2\right)\)